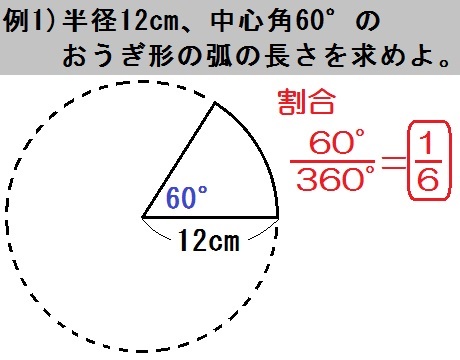
中1数学 中学数学3分で簡単にわかる!「扇形(おうぎ形)の面積の求め方」の公式 中1数学 中学数学速さの単位変換・換算の2つの方法弧度を使って弧の長さと面積を求める このテキストでは、弧度を使って弧の長さと面積を求める方法を解説しています。 半径がrで中心角がθの扇の弧の長さをl(扇形の中心角)=(円弧の長さ)/(半径) ラジアン =(180/π)×(円弧の長さ)/(半径) 度 (円弧の長さ)=2π×(半径)×(中心角の比) (中心角の比)=(中心角)/(全円の中心角) ただし、中心角は度またはラジアンのどちらかに統一する。 単元:おうぎ型の中心角の解き方 問題 半径9㎝、弧の長さが6n㎝のおうぎ形の中心角を求めなさい。 中学生数学特訓プラン 基礎力養成特訓プラン 推奨学年中学1年~中学3年生内容計算の基礎養成演習時間割

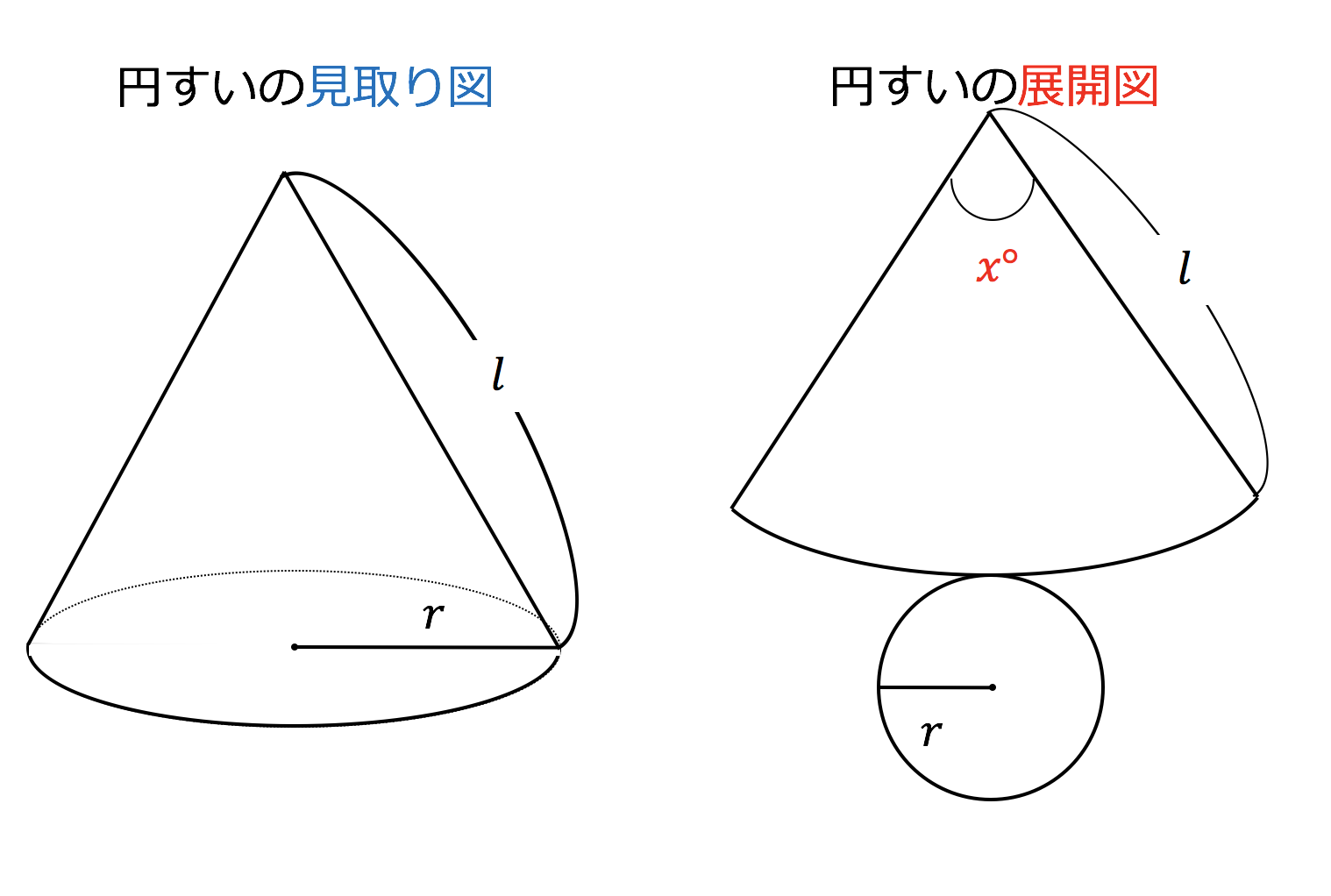
円すいの側面積と展開図の中心角 たぬぬ塾 中学校の先生たち
中1 数学 扇形 中心角 求め方
中1 数学 扇形 中心角 求め方- 元の円が360度で、この扇形の中心角は90度なので、 (90÷360)×100=25 つまり、この扇形は元の円の25%と考える事ができます。 ですから この扇形の面積=もとの円の面積×25% この扇形の弧の長さ=もとの円の円周×25% と計算することができます。 たとえば、半径3cmで中心角1度の円の面積を求めなさいという問題が出題されたとします。 円周率=314で考えましょう。 この円全体の面積は 円の面積=半径×半径×円周率で導き出せます。 円の面積=3×3×314 つまり26㎠です。 扇形の面積はこの円の1




おう ぎ 形 面積 求め 方 運転手 ニュース
中心角の簡単な求め方教えてください! 上本 き形の中心久の求め方 しpro 半径5cm, 弧の長さご 4z cm のおうぎ形0 申訪角の大きさを求めます。 円とおうぎ形 中心角 簡単な 求め方数学Ⅱ(三角関数):円弧の長さと扇形の面積(弧度法) オンライン無料塾「ターンナップ」 対象 高2 再生時間 328 説明文・要約 〔半径 r、中心角 θ(ラジアン)の扇形について〕 ・円弧の長さは rθ 円周の長さ 2πr に対して、中心角の カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる Study 円錐の側面 扇形 の中心角の求め方 中2数学
ベストアンサー率25% (45/175) 円の面積=半径×半径×円周率 円全体の中心角は360° 中心角1°の面積は円の面積÷360°×1°=半径×半径×円周率÷360°×1° 中心角60°の面積は、中心角1°の面積÷1°×60°=半径×半径×円周率÷360°×60° 同じ半径を持つ円と扇形を比べることで、中心角を求めるという考え方です。 半径が9㎝の円の円周の長さは、\(2\times \pi\times 9=18\pi(cm)\) 半径が9㎝の扇形の弧の長さは、問題文より \(3\pi(cm)\) です。中1数学 「おうぎ形の中心角の求め方」について① 今回の中1数学の解説は「おうぎ形の中心角の求め方」についてです。 弧の長さや面積が与えられている時どのようにして中心角を求めるのかを確認していきましょう。
円すいの展開図、中心角の公式を知って5秒で解こう♪ 面積 面積 円すいの展開図の中心角を求めなさい。 円周率は314とします。 知りたがり 何に注目 すれば中学数学平面図形 おうぎ形の中心角の求め方 平面図形 おうぎ形の中心角の求め方 おうぎ形の中心角を求める問題で,わかっている数字が変わると求め方がわからなくなります。(1) 中心角と半径が同じなので、扇形 は合同になります。 よって、中心角が同じの同一円上の弧と弦の長さは等しくなります。 (2) 弧と半径が同じなので、扇形は合同になります。 よって、中心角が同じの同一円上の中心角と弦の長さは等しくなります。 (3)




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




扇形や円の問題と図形の回転移動 駒澤塾 中学受験の算数 理科
採点する やり直す 解説 3 半径 10 ,中心角が90°の扇形の面積 円の面積の4分の1だから,10 2π ÷4=25 π π 採点する やり直す 解説 4 下の図の灰色で示した図形の面積 扇形の面積は円の4分の1で25 π ,これから三角形の面積 10×10÷2=50 を引く「ある点が、扇形の中にあるか?」を判定するプロセス 扇形に対する内外判定は以下のプロセスで行います。 (1) その点は、扇形が属する円の中にあるか? (2) 扇型の中心角は180°未満か? ・中心角が180°未満であれば、 (3) その点は開始角より左側にあるか? 中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも 平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト おうぎ形 中心角を求める3つのパターンを解説




超簡単 扇形 楽勝 中心角の求め方 Youtube




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
「扇形の弧の長さ」の求め方の基本はわかったね?? それじゃあ、 扇形の弧の長さの公式 をみていこう! 扇形の半径をr、中心角をα、円周率をπとすると、 2πr×α/360 で「扇形の弧の長さ」を求められるんだ。 既に知ってる「扇の中心角を求める問題」に変えてしまう っていうのがポイント! 扇の中心角の求め方を知らない人は、 扇形の中心角の求め方3パターンを見てみてね ちなみに、中心角を求める公式もあって $中心角 = 360 \times \dfrac{半径}{母線}$中1数学まとめ(解説と問題) 割合とパーセントが苦手な人のための練習問題(中学生用) 中1数学・文字式の利用〜3つの連続する整数の和が3の倍数であることの証明 奇数、3の倍数、2桁の自然数などのnを使った表し方(文字式の利用) 正負の数の計算




印刷可能 円錐 中心角 求め方 比




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学
演習問題で理解を深める! (1)半径6㎝、中心角1°のおうぎ形の弧の長さと面積を求めなさい。 (1)解説&答えはこちら 答え 弧の長さ: 面積: 弧の長さを求めるためには の公式にあてはめます。 円の面積を求めるためには の公式にあてはめます。 (2)半径4㎝、中心角45°のおうぎ形の弧の長さと面積を求めなさい。ちくらっぽインク したこと ピグストーリー じゃがいも君の絵日記 KYな会話 などなどを収録したchikurappo,incです。 まずは一般的な方法で解いてみましょう。 底面の半径が3cmなので、円周=直径× =6 cm となります。 底面の円周とおうぎ形の孤の長さは等しいので、孤の長さも6 cmです。 そこから、半径12cm&孤の長さ6 cmのおうぎ形の中心角を逆算して求める──これが一般的な解き方です。 このやり方では、ちょっとした方程式も出てくるので、早い方でも秒、ゆっくり解くと1




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




おうぎ形の中心角の求め方 Youtube
扇形の中心角を求める問題です。 扇形の面積が分かっているときは、 円の面積と扇形の面積を比べて、扇形が何倍になっているのかを調べます。 扇形の弧の長さが分かっているときは、 円の周の長さと扇形の弧の長さを比べて、扇形が何倍になっているのかを調べます。 扇形の割合が分かったら、中心角を求めていきます。 扇形の中心角 (PDF) Tweet 登録カテゴリ中心角 面積 (3) 半径8cm、弧の長さ4πcm 中心角 面積 2 次のようなおうぎ形の中心角と弧の長さを求めなさい。ただし、円周率をπとする。 (1) 半径6cm、面積4πcm2 中心角 弧の長さ (2) 半径6cm、面積10πcm2 中心角 弧の長さ (3) 半径8cm、面積8πcm2 中心角 弧の扇(おうぎ)形の面積を求める公式3つと弧の長さの求め方をお伝えします。 面積と弧の長さは比例ですべて解けるのですがこれを苦手にしている中学生はものすごく多いです。 これには当然とも言える理由が3つあります。 ここで図形を



Math 円錐の展開図の中心角と母線 半径 中学生 働きアリ




中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube
最高 50 扇形 の 中心 角 求め 方 簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを 問題 1 半径が 3cm弧の長さが 3π cm のおうぎ形の中心角を求めなさい 2 半径が 4cm弧の長さが π cm のおうぎ形の中心角を求めなさい 3 半径が 2cm弧の長さが π2 cm 扇形の中心角を求める公式は、 x = 180 × 弧の長さ π × 半径 x = 180 × 弧 の 長 さ π × 半 径 弧の長さ= L、半径= r とすると、 x = 180L πr x = 180 L π r だよ さっきの「半径4cm、弧の長さ6π cmの扇形」の中心角を求めてみるよ。 中心角はつぎの3ステップで計算できるんだ。 Step1 扇形の中心角をx°とおく まずは「扇形の中心角」を「x°」とおいてみよう。 これは 方程式の文章題 と同じ。 Qikeru:学びを楽しくわかりやすく 5 Pockets 方程式の利用一次方程式の文章題の4つの解き方




扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト



側面のおうぎ形の中心角を求めなさいという問題があるのですが全くわか Yahoo 知恵袋
数学・算数 中1 数学 扇形 中1 数学 扇形 半径 3cm 中心角 60°↑この問題の解き方(途中式)を 9 この半円の半径と、 EHGの面積のJan 05, 136 半径3cm、弧の長さ5πcmの扇形の面積の求め方を詳しく教えてください 7 半径と面積が分かっているときの中心角の求め方 8 半径12cmで中心角が、60度のおうぎ形に 中学1年生 中1 数学 表面積の求め方 表面積の求め方と! 円錐の側面積と中心角の簡単な裏ワザをごしょーかい! ページ数少ないです笑 塾で教えてもらいました ( ( ( ( 中1 数学 表面積 求め方 まとめ 裏ワザ 簡単 側面積 中心角 math このノートが参考になったら、著者をフォローをしま 求めたい半径の大きさを ㎝とすると 半径が ㎝で中心角が1°の扇形の面積は と、表すことができます。 そして、面積が ㎠になるはずだから という二次方程式が完成します。 あとは、これを解いていけば の値(半径)を求めることができます。 この




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



中学数学 平面図形 のコツ 円とおうぎ形




50 おうぎ形 中心角の求め方 公式 最高のぬりえ



3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




標準 おうぎ形と正方形の面積 なかけんの数学ノート




中1数学 おうぎ形の公式 例題編 映像授業のtry It トライイット




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



3
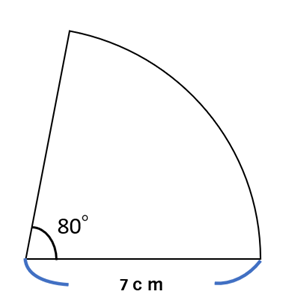



今さら聞けないシリーズ 小6 中1数学 おうぎ形の弧の長さと面積で混乱するのはなぜか その対策をお伝えします マナビバ Com




おう ぎ 形 面積 求め 方 運転手 ニュース




7 と 11 の求め方を教えてください Clear




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ



1




Study 円錐の側面 扇形 の中心角の求め方 中2数学 ちくらっぽインク




中1数学 おうぎ形の応用問題 練習編 映像授業のtry It トライイット




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋




扇形の中心角の求め方を教えてください Clear




中学数学 円錐の中心角の求め方 3パターン なぜか分かる はかせちゃんの怪しい研究室




おうぎ形 半径の求め方 数学の記録




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学



3




T11 D Descubre Como Resolverlo En Qanda




扇型の求め方や中心角の求め方も分からないので 解説もお願いします この問題の答えは Clear



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋




3の扇形の中心角が90度になる理由を教えてください 3の扇形の中心角が 中学校 教えて Goo




中学数学 弧の長さから中心角や面積を求める Youtube



Math 円錐の展開図の中心角と母線 半径 中学生 働きアリ



カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円すいの側面積と展開図の中心角 たぬぬ塾 中学校の先生たち
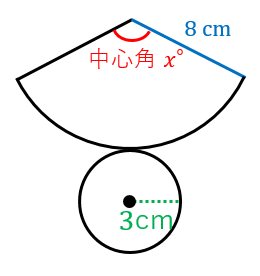



円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




中1数学 おうぎ形の中心角の求め方 について ひっそりと物理や数学を解説する




扇形の弧の長さの求め方 公式と計算例



中1の数学についてです 中心角が45度で 弧の長さが3p の扇形 Yahoo 知恵袋




1分でわかる 扇形の中心角の求め方 Youtube




扇形の弧の長さの求め方 たぬぬ塾 中学校の先生たち
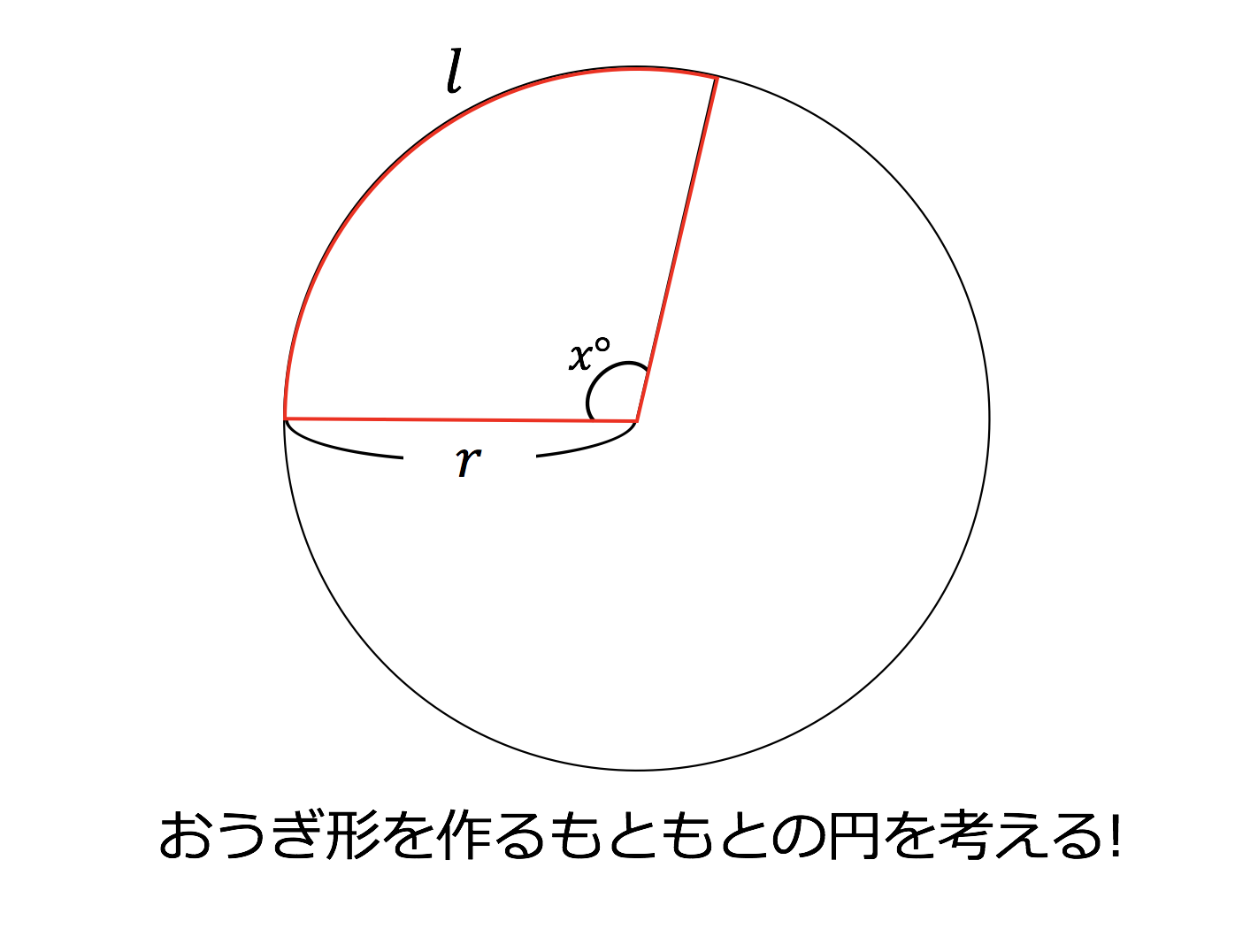



3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中学数学 扇形の中心角の求め方3パターン ピザでわかる なぜか分かる はかせちゃんの怪しい研究室




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
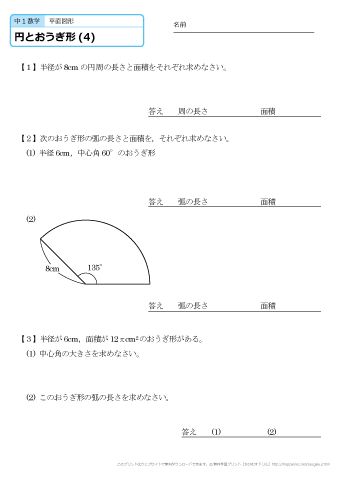



中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




公式を図解 すい体の体積 円すいの表面積の求め方




円錐の側面積 展開図の扇形の中心角 半径 母線を軸として解く 身勝手な主張




高校入試対策数学 円錐に関する対策問題 Pikuu



1




扇形の弧の長さの求め方 公式と計算例




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
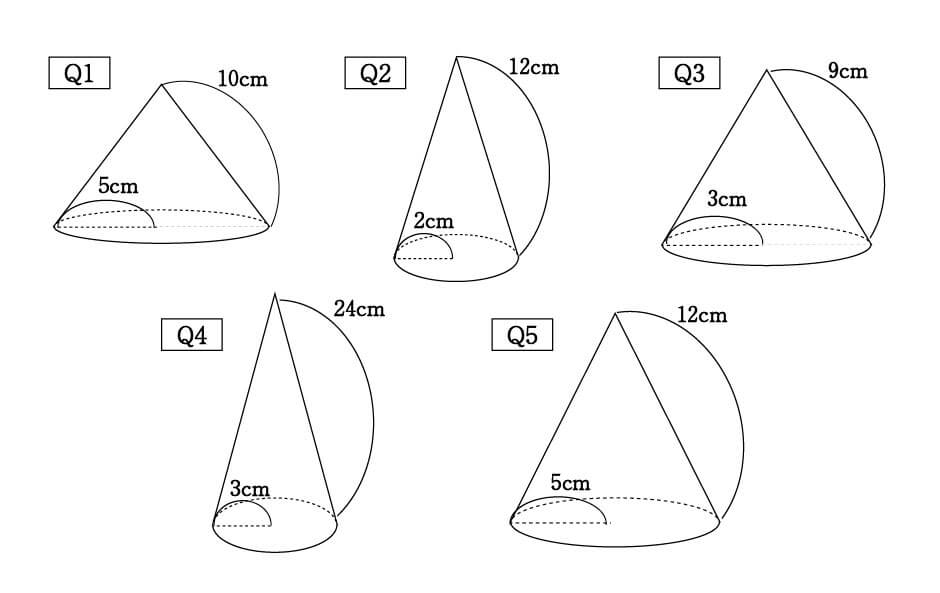



数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ
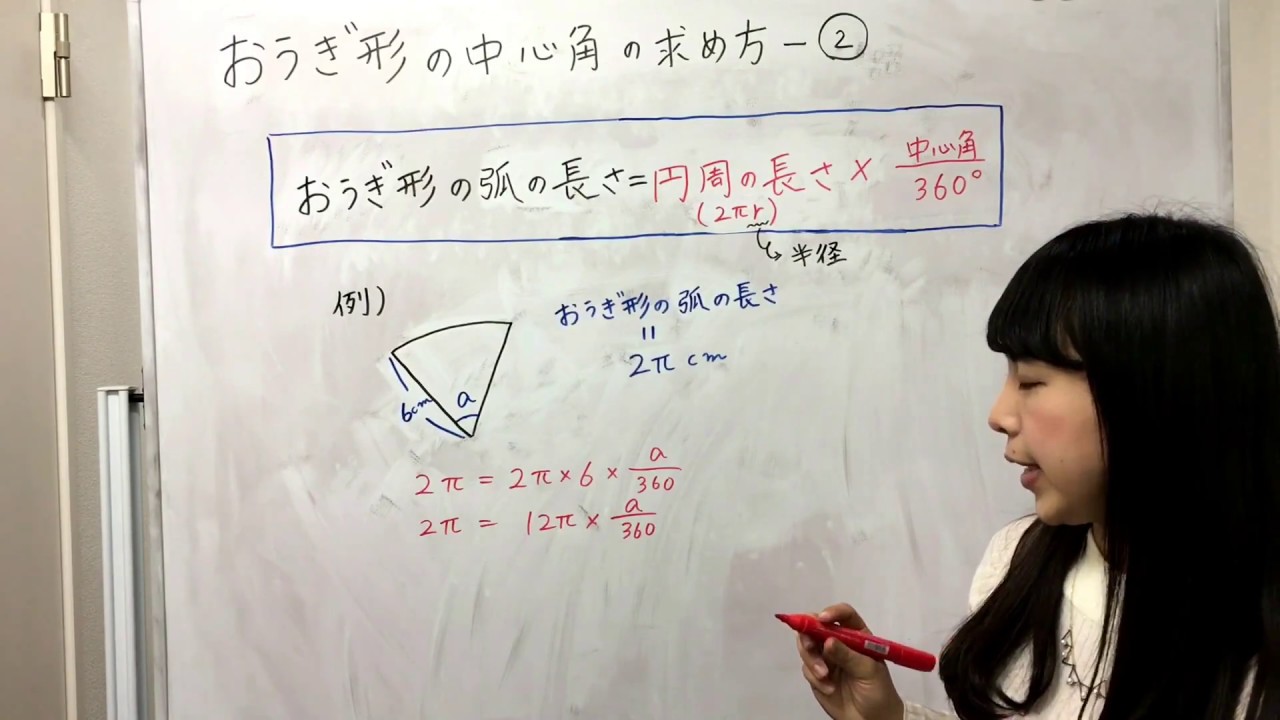



中1数学 おうぎ形の中心角の求め方 家庭教師のガンバ Youtube




円 扇形 の面積 周や弧の長さの公式 数学fun
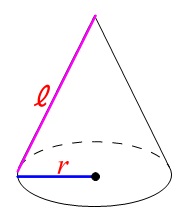



扇 おうぎ 形の面積を求める公式と弧の長さの求め方




中心角の求め方が即わかる 合わせて知りたい知識とは 高校生向け受験応援メディア 受験のミカタ




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




この 中心角の求め方を教えてください 1 の方です Clear



面積 これが中学入試に出た図形問題




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学



ダウンロード 扇形 中心 角 求め 方 ニスヌーピー 壁紙



半径1 中心角60 のおうぎ形に内接する円の半径を求める 数楽者のボヤキ ツブヤキ ササヤキ 中学 数学 道徳 Mathematics Puzzles




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




中1です お願いがあります 扇形の中心角の求め方を Clear
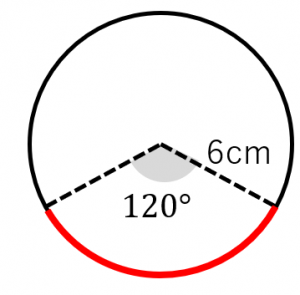



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
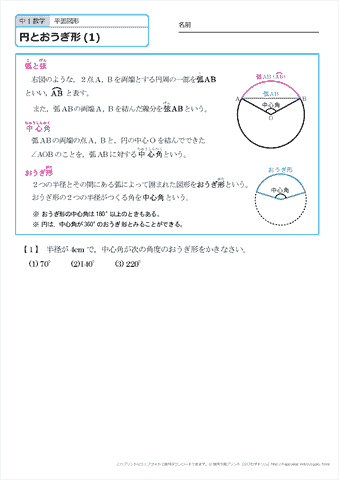



中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち




中1数学 おうぎ形の応用問題 練習編 映像授業のtry It トライイット




中心角の新着記事 アメーバブログ アメブロ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




中1 数学 空間図形9 おうぎ形の公式 17分 Youtube



半径10センチ 中心角90 の扇形oabの内部にoa Obを直径と Yahoo 知恵袋
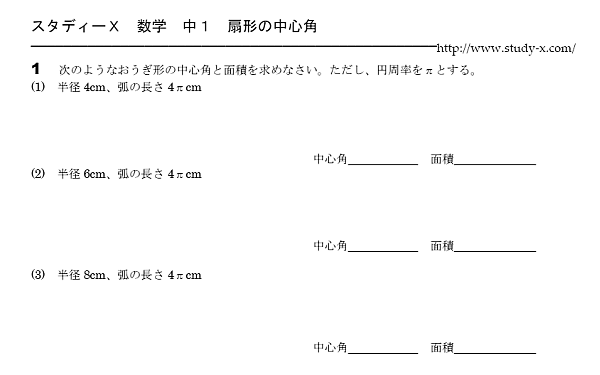



扇形の中心角 無料学習プリント教材




3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ




おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト



半径4cm 中心角225 のおうぎ形の弧の長さと面積の求め方と答 Yahoo 知恵袋



0 件のコメント:
コメントを投稿