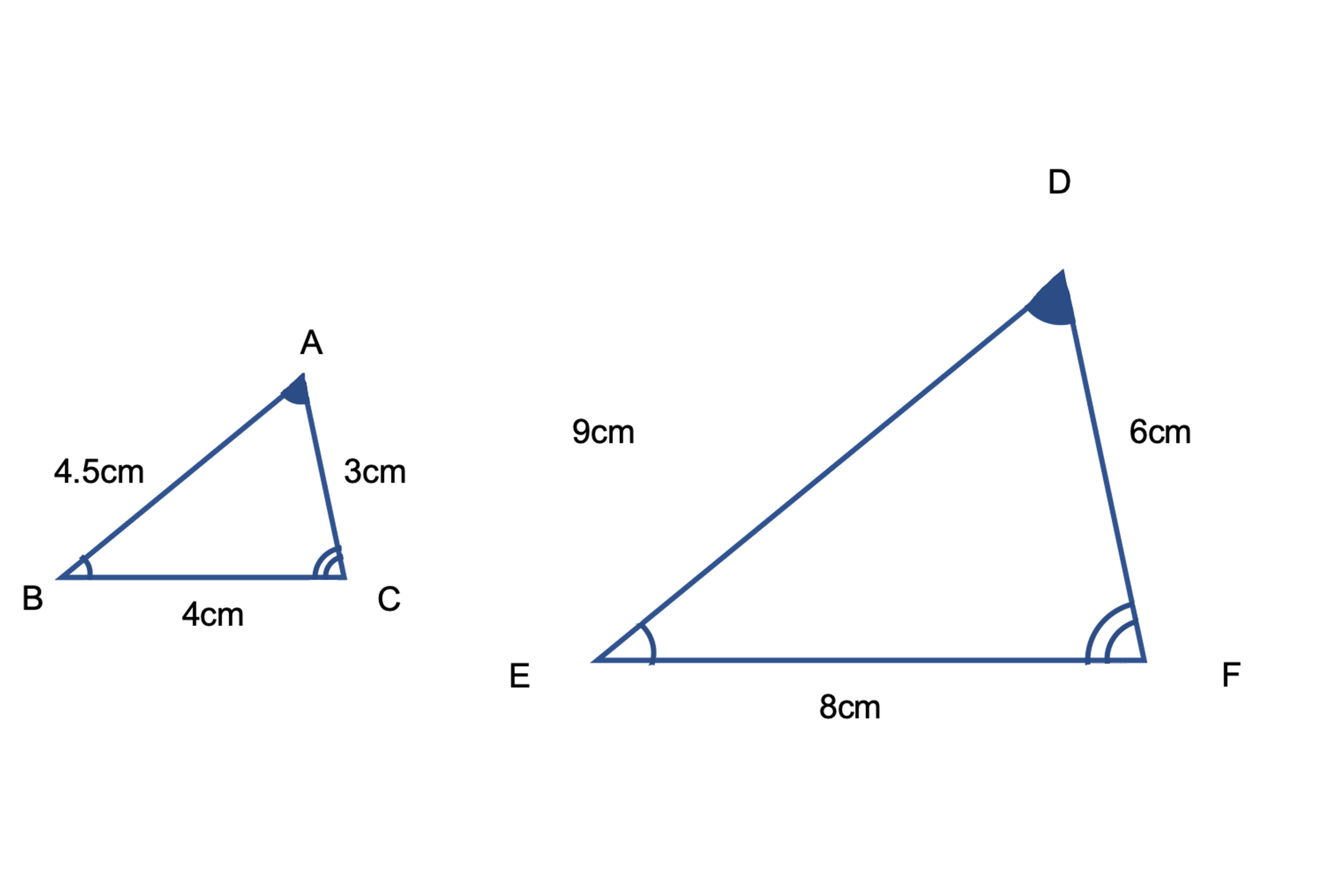
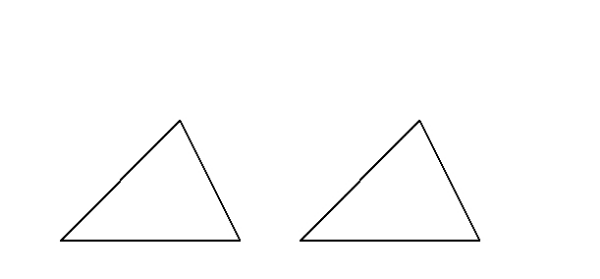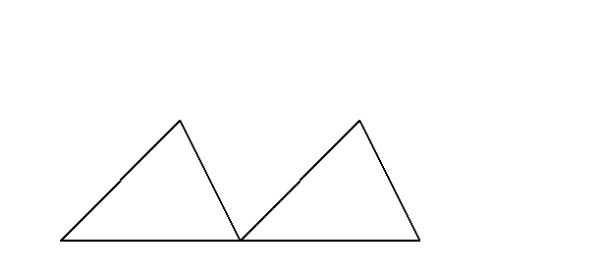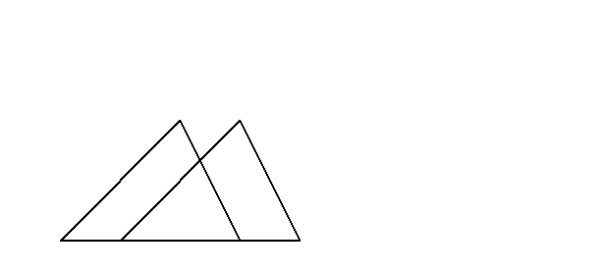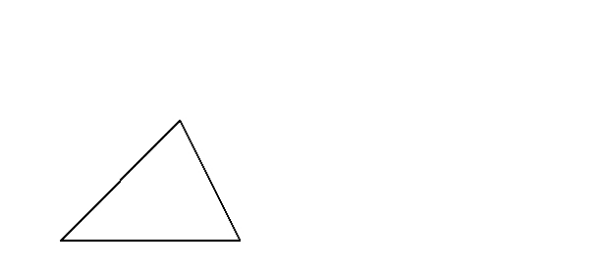
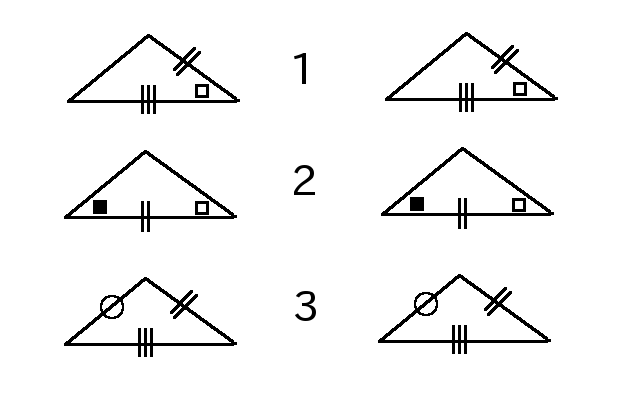
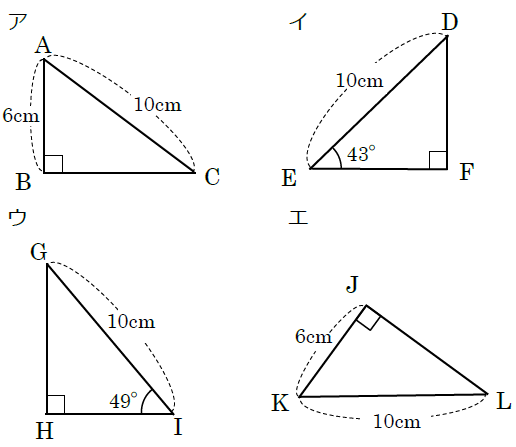
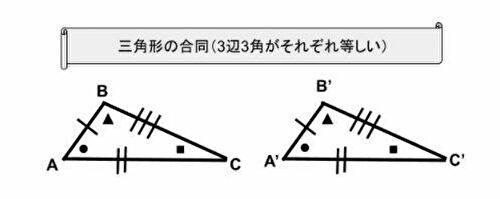
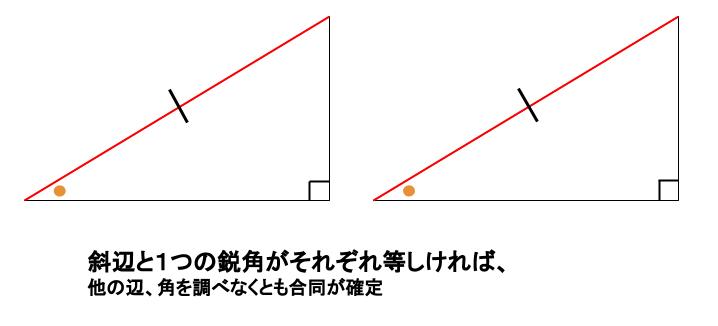
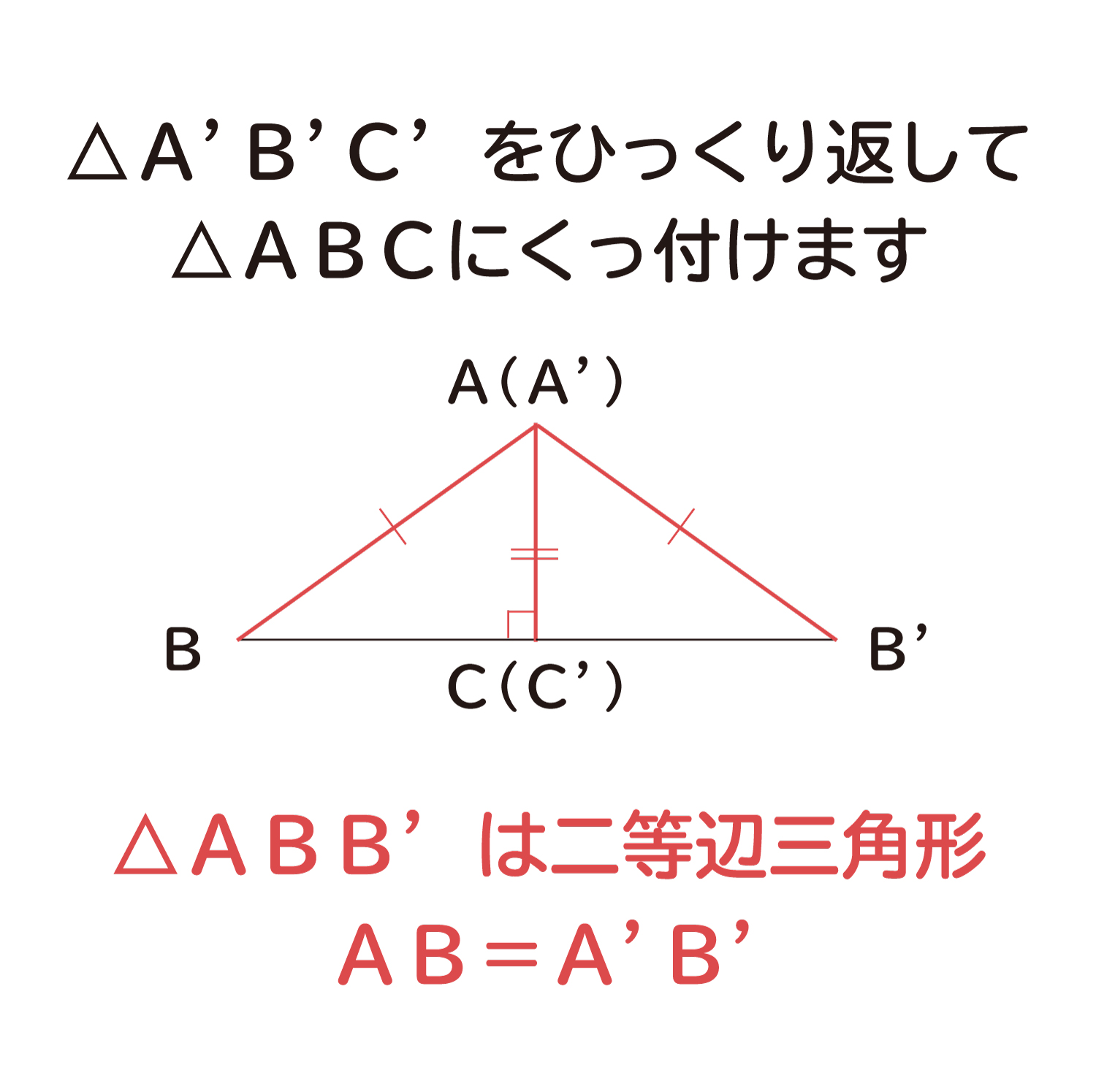
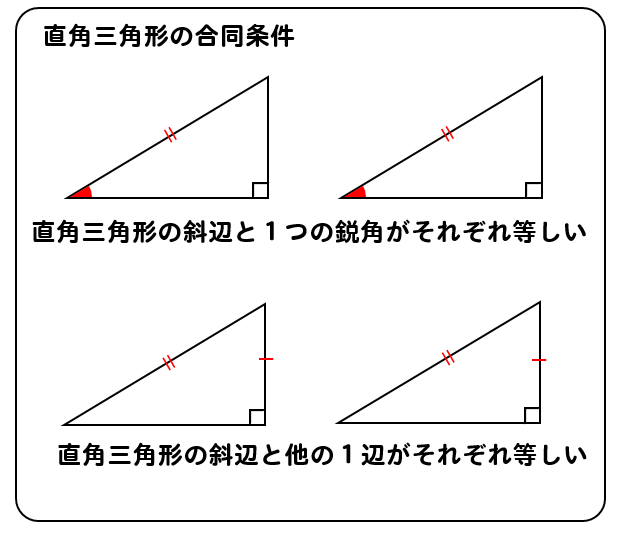
三角形の合同条件 とは、 2つの三角形が合同であることを示すための条件 です。 以下の3つの合同条件のうち、どれかが成り立つ場合、その三角形は合同であるといえます。 3組の辺がそれぞれ等しい。 2組の辺とその間の角がそれぞれ等しい。 1組の辺とその両端の角がそれぞれ等しい。 直角三角形の合同条件は、次の2つです。 斜辺と1つの鋭角がそれぞれ等しいAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators角度についての条件はなし 2 2 つの三角形があって、どちらも 1 1 辺は 10cm 10 c m で等しいんだ。 これだけの情報では、 2 2 つの三角形が合同であるとは確定できませんね。 「 1 1 つの辺が等しい」だけでは、合同が確定するためには、条件が少なすぎます

Download 中2数学 三角形 直角三角形の合同条件の覚え方のポイント Images For Free
合同 の 三角形 条件
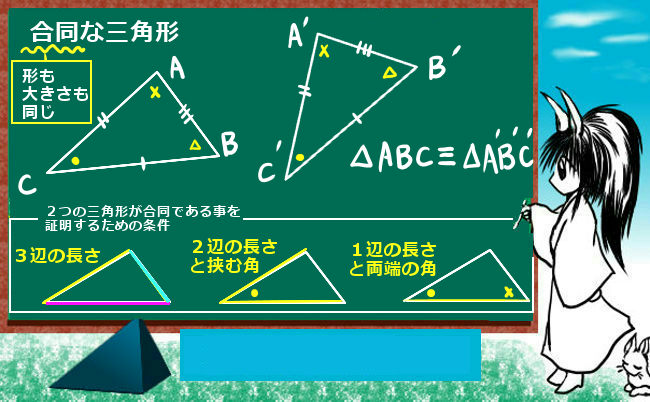
合同 の 三角形 条件-三角形の合同条件とは? さて、合同な三角形は3つの角と3つの辺が等しくなっているという性質があることが分かりました。 では逆に、2つの三角形が合同であると示すためには、その3つの角と3つの辺を全て分かっている必要があるのでしょうか? 実は、そうではないのです。ある辺の数と角の数だけ等しいことが分かっていれば、その図形が合同であると示すこと 合同条件を満たすとなぜ合同なのか?を考えてみる まずは、三角形の合同条件についての復習 まずは、"合同"についての復習です。 "合同"とは、簡単に言えば、2つの図形を比べたとき、形と大きさが同じであることをいいます。 言い換えると、一方の図形を動かしたり裏返したりすると



記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス
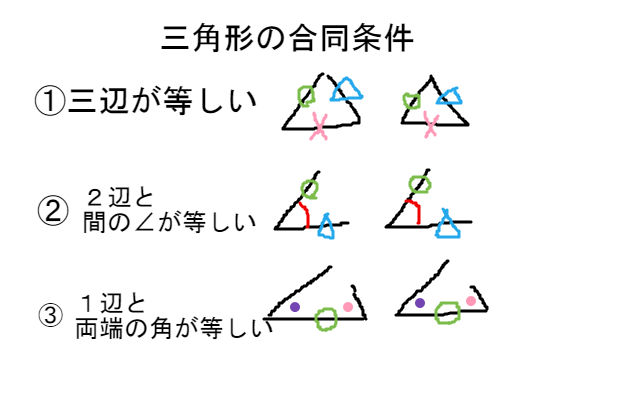
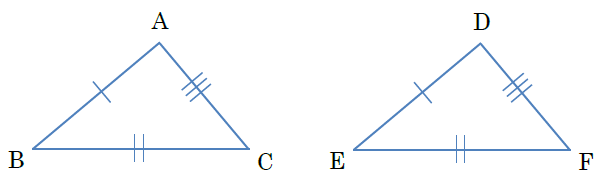
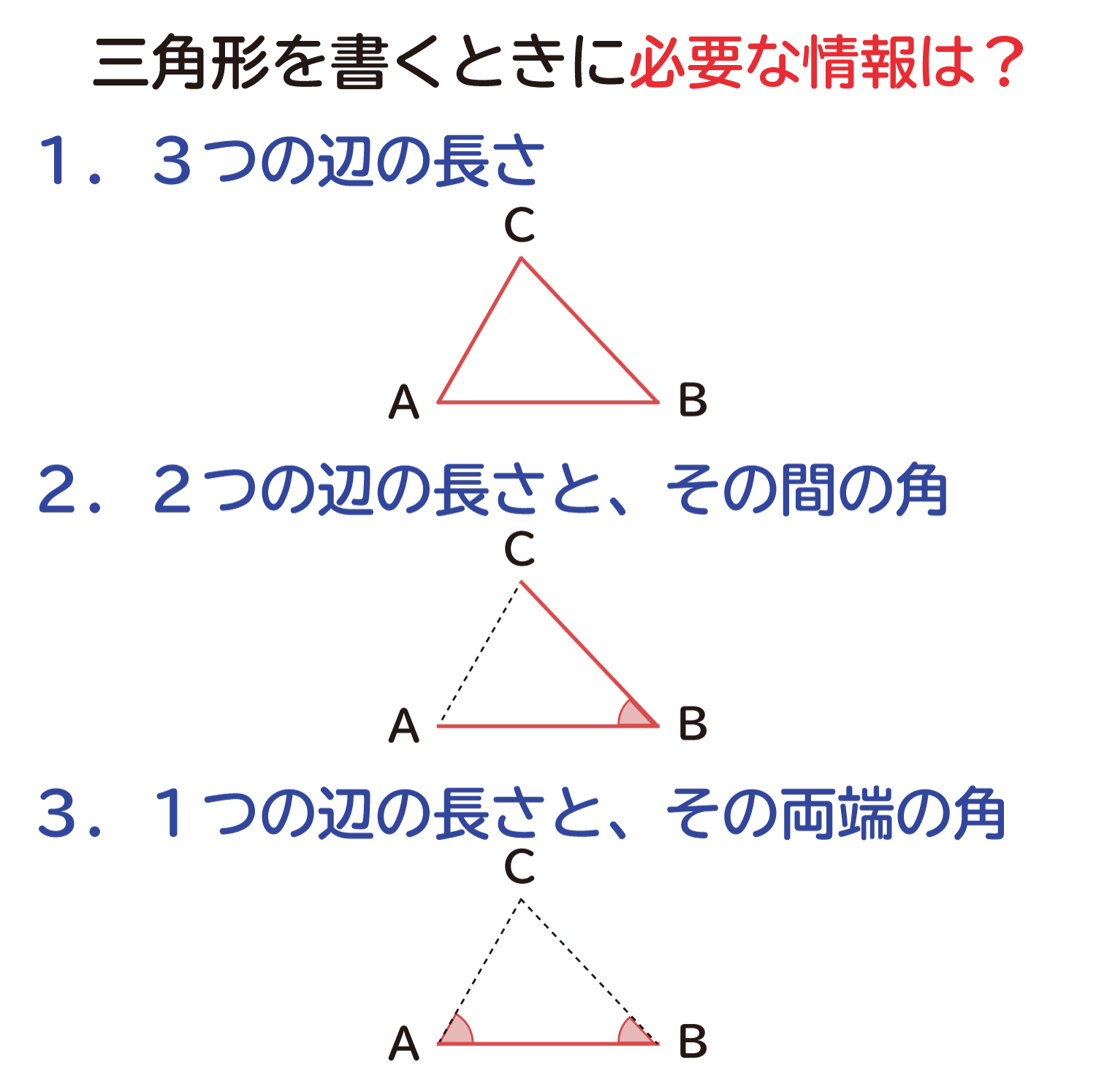
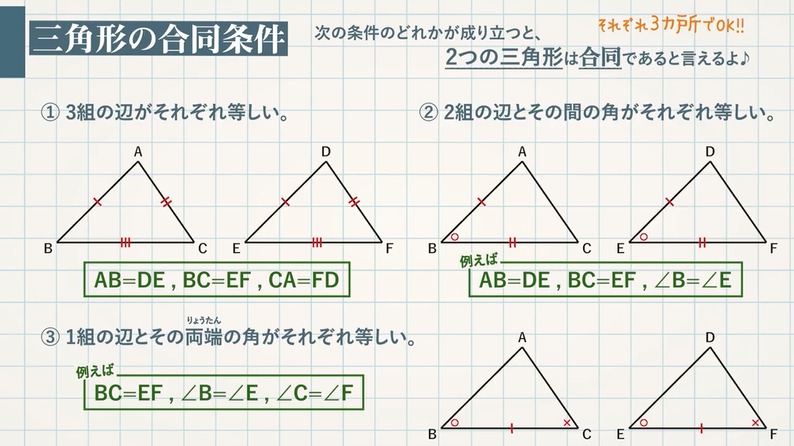
中学数学で、三角形の合同条件を学習します。 2つ三角形があったときに、一方が他方にぴったりと重なることを合同といいます。 合同な三角形は、重なり合う辺の長さは同じ長さですし、重なり合う角の大きさも同じ角度になっています。 3つの辺を差しで長さを測り、3つの角の大きさを分度器で測ると、合同か合同でないかを判断できるわけですが 三角形の合同条件を考えると、まずひとつ目は 「3組の辺の長さがそれぞれ等しい」 。 ふたつ目は 「2組の辺と、その間の角が等しい」 。 そして最後が 「1組の辺と、その両端の角が等しい」 になります。About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru よって、三角形の合同条件、3つの辺の長さが等しいならば合同なので(SSS)、\(\triangle ABC,\triangle DEF\)は合同です。 合同な三角形の対応する角度は等しいので、\(\angle ACB=\angle DFE=90^{\circ}\)であることが示せました。 以上、ピタゴラスの定理の逆の証明を紹介してきました。 「直角三角形ならばステップ1 三角形の合同条件(2分23秒) 4/5 ステップ2 同じ部分を見つけ出す(3分10秒) 5/5 ステップ3 パパッと分かる問題を解く(2分28秒
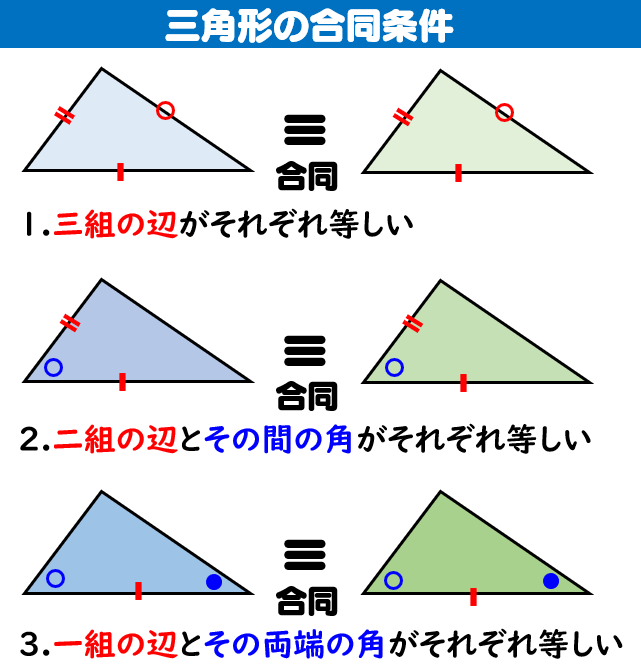
三角形の合同条件 3組の辺がそれぞれ等しい 2組の辺とその間の角がそれぞれ等しい 1組の辺とその両端の角がそれぞれ等しい これから証明問題へ進んでいく上で 必要となってくるものなので ぜーーーーったいに覚えておきましょう! また、合同な1つの三角形の3つの辺は、もう1つの三角形の3つの辺と正確に同じ長さである。 一方の3つの角は、それぞれ他方の角と同じ角度である。 三角形の合同の仮定 2つの三角形が合同であることを見つけるには、5つの方法があります。 SSS (Side Side)、または Side Side直角三角形の合同条件 2つの直角三角形は、次の場合に合同である。 1 斜辺と1つの鋭角が、それぞれ等しいとき(証明) 2 斜辺と他の1辺が、それぞれ等しいとき(証明)



合同とは 相似とは




Download 中2数学 三角形 直角三角形の合同条件の覚え方のポイント Images For Free
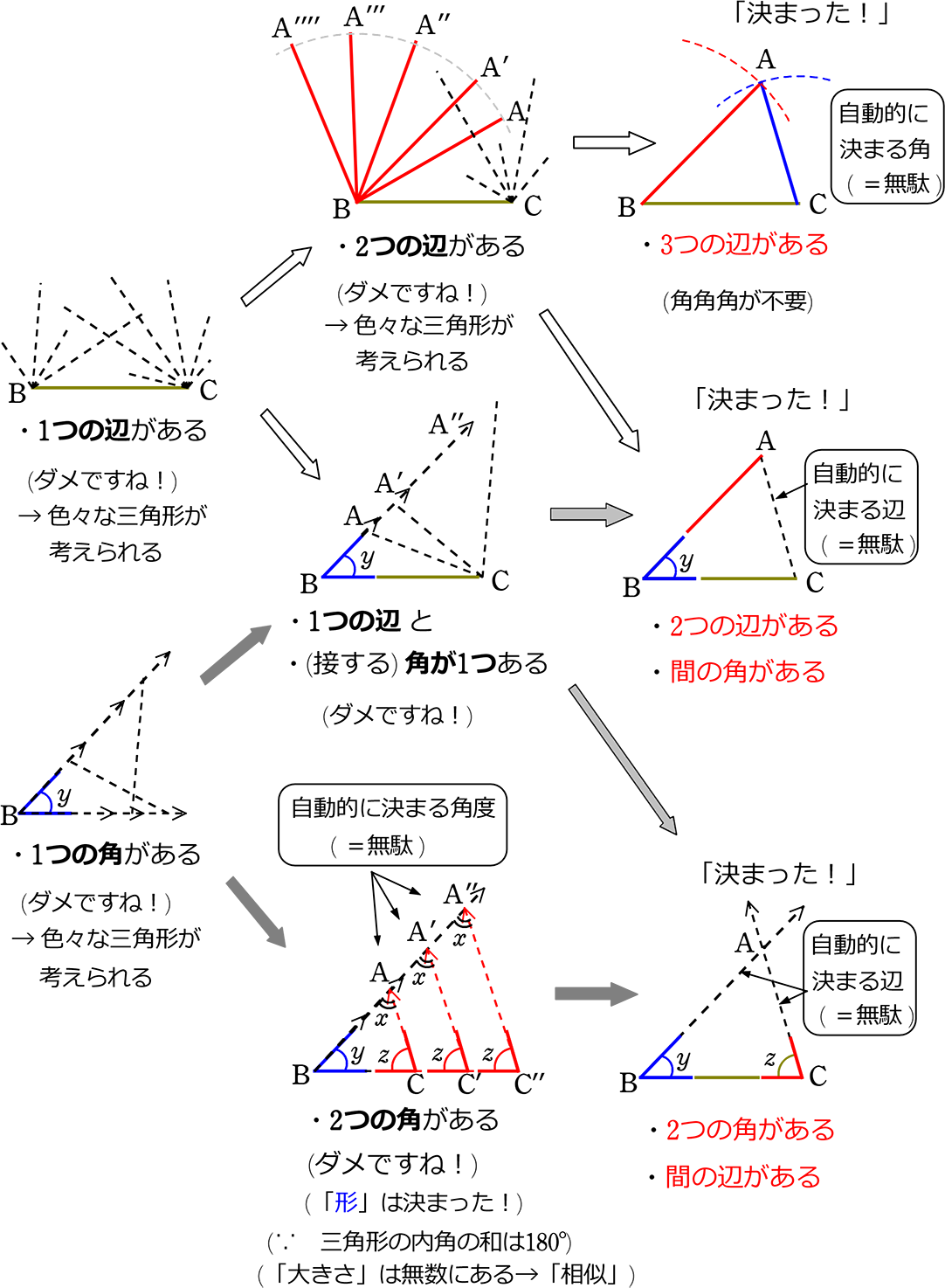
よって、「直角三角形の合同条件」は「三角形の合同条件」を さらに絞ったものと言うことができますね もちろん、証明できるなら、普通の「三角形の合同条件」で証明しても全く構いませんね (直角三角形) ・釣り竿の「角度だけ」で、「形」が決まる ・さらに釣り竿の「長さだけ」で 中学数学:攻略・三角形の合同 年3月30日 22年5月29日 こんにちは。 相城です。 今回は三角形の合同の証明の攻略法を見ていきましょう。 動画でご覧になりたい方は下部に載せていますのでご覧ください。 それではどうぞ。三角形の合同条件 合同とは 一方の図形を移動させて他方に重ね合わせることができる場合、この2つの図形は 合同 であるという。 三角形の合同を判断する場合、重ねあわせなくても下記の3つの合同条件のうちどれか一つに当てはまれば合同だといえる。 三角形の合同条件 3組の辺がそれぞれ等しい。 2組の辺とその間の角がそれぞれ等しい。 1組の辺とその両端の角がそれぞれ等しい。 例 56°



三角形の 合同条件 相似条件 の意味について 三角比や正弦定理 余弦定理の理解も深くなる ここからはじめる高校数学
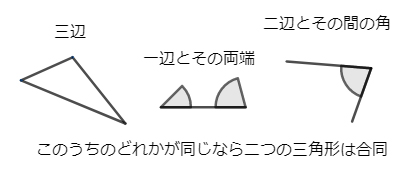



数学のアレ 何に役立つ 三角形の合同条件 同じ形の三角形を見つけて テストで5点くらいもらう 以外の使い方 1 2 ページ ねとらぼ
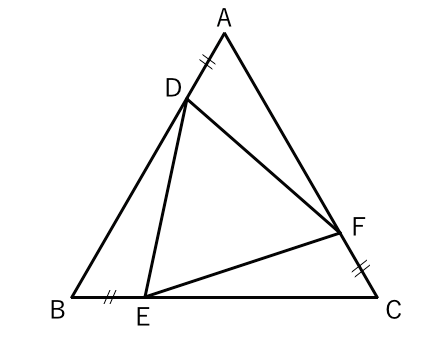
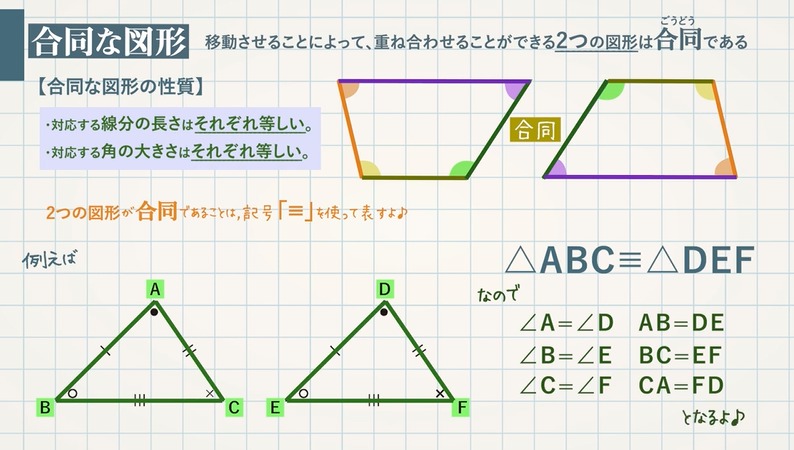
二等辺三角形・正三角形の合同の証明 問題はこちらです。 問題 図で ABCは正三角形である。辺AB、BC上に るとき、次の問いに答えよ。 (1)AE=CDであることを証明せよ。 解答・解説は下にあります。 "合同の証明⑩" の 続きを読む アクセス 住所 埼玉県 検索 検索 検索 このサイト 三角形の合同条件 合同な図形 2つの合同な図形は、その一方を移動して、他方にぴったりと重ねることができる。このとき、重なりあう頂点、辺、角を、それぞれ対応する頂点、対応する辺、対応する角という。 合同な図形について、次のことが成り立つ。 合同な図形の性質 合同な図形で合同な図形の性質 ・対応する線分の長さはそれぞれ等しい。 ・対応する角の大きさはそれぞれ等しい。 2 つの図形が合同であることは、記号 「≡」 を使って表します。 例えば、 ABCと DEFという 2 つの三角形が合同であるときは、 A B C ≡ D E F と表します。 これら 2 つの三角形は、合同な図形の性質より、 ∠ A = ∠ D , ∠ B = ∠ E , ∠ C = ∠ F A B = D E , B C = E F , C A = F D となります。 三角形の




直角三角形の合同条件 算数 数学が好きになりmath
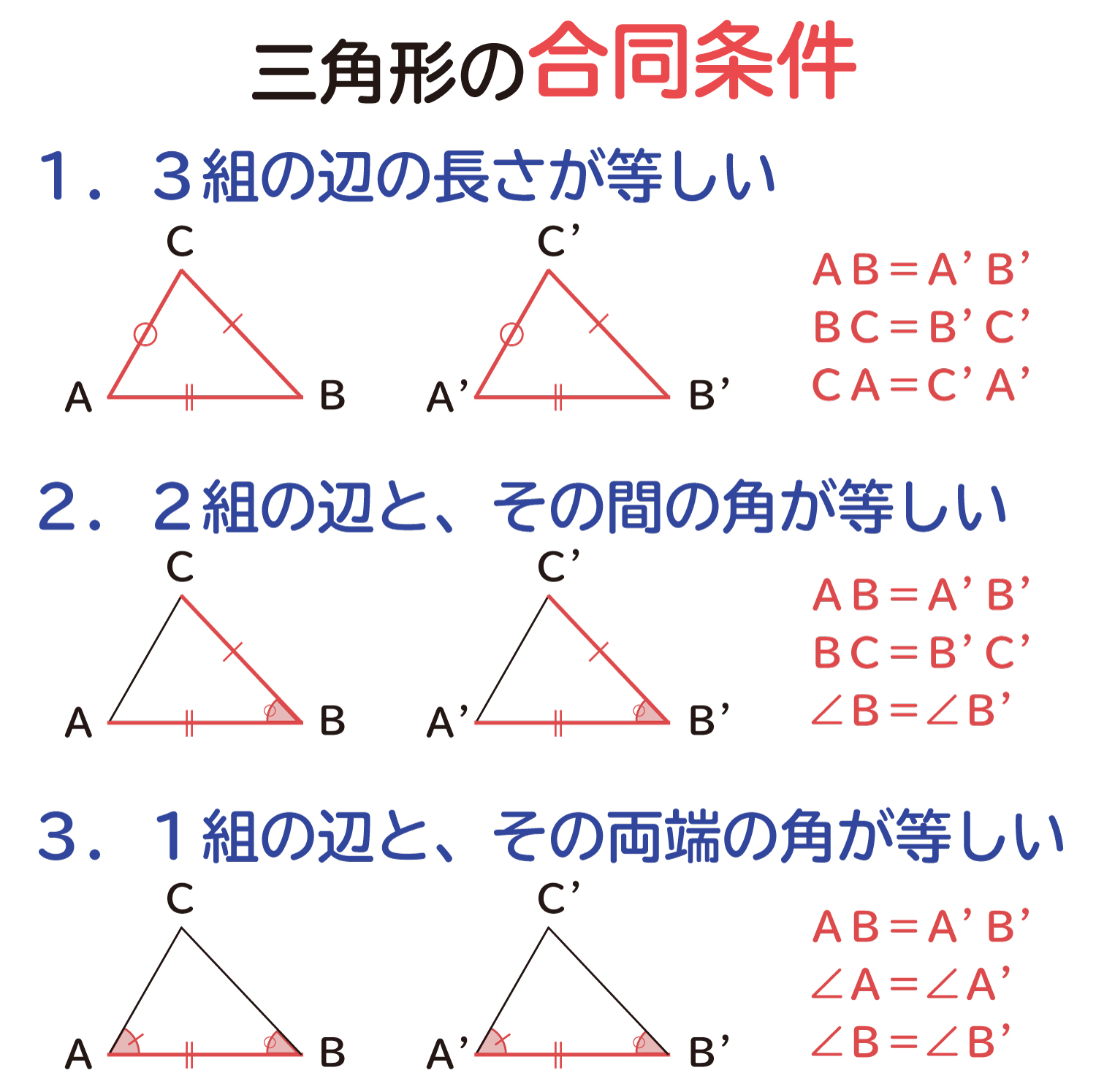



三角形の合同条件の説明 おかわりドリル
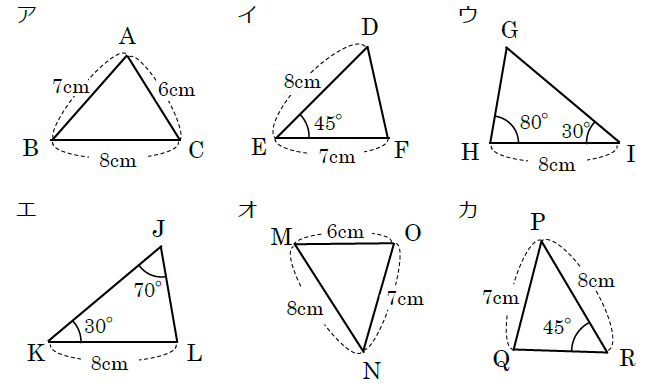
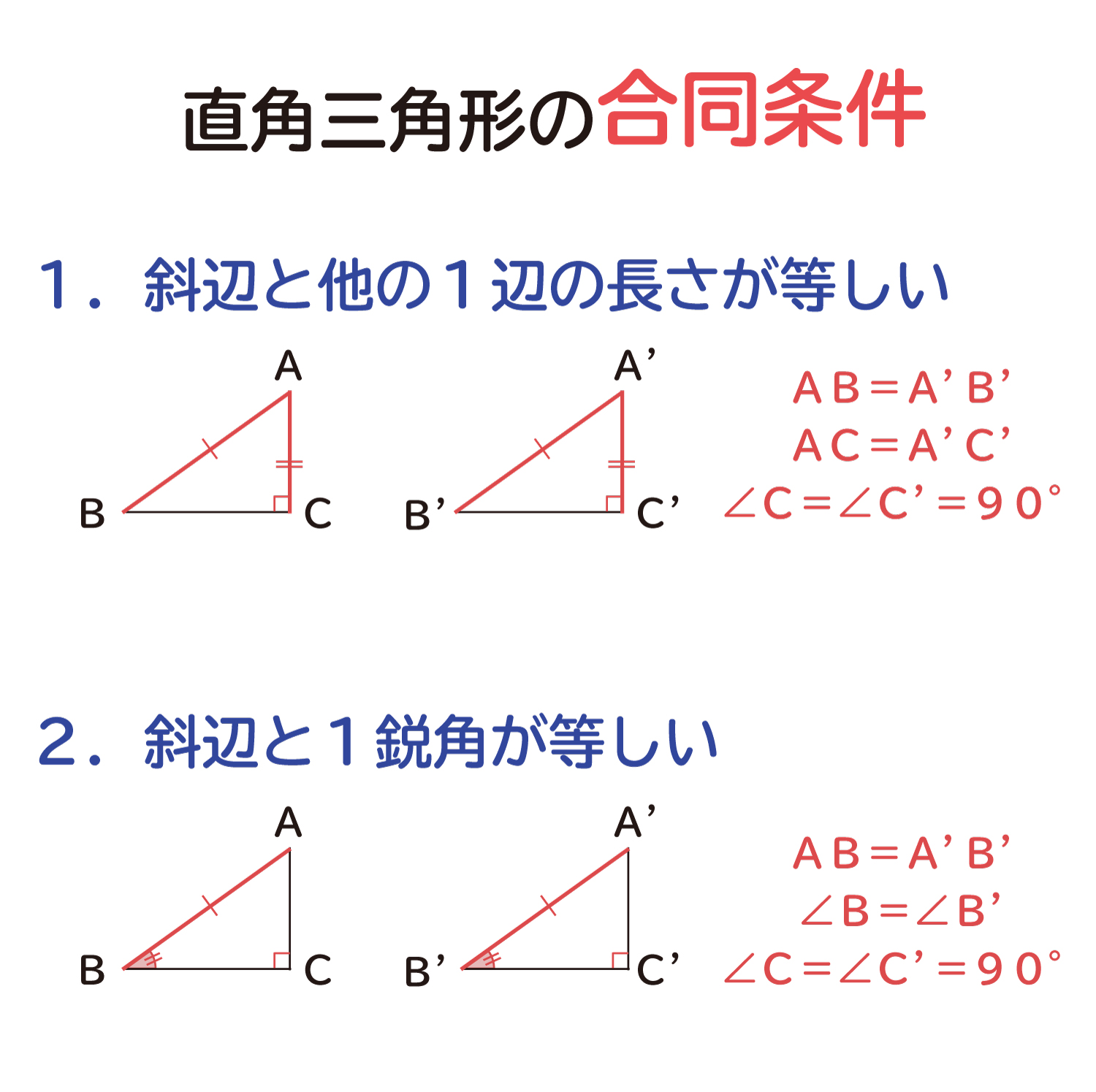
直角三角形の合同条件とは 直角三角形は、以下のことが分かれば合同だと言えます。 今までの三角形の合同条件が このように、3つの情報を組み合わせて合同を言うことができましたが 直角三角形の場合には このように2つの情報だけでOKになります 三角形の合同条件は以下の3つですね。 三辺が等しい。 二辺とその間の角(二辺夾角)が等しい。 一辺とその両端の角(二角夾辺)が等しい。 これも丸暗記でもいいですが、文字だけ見てもなかなか覚えられないですよね。3つの辺の長さがわかっているときの、合同な三角形の作図をする問題を集めた学習プリントです。 『例題』と『確認』では、定規・コンパスの使い方をなぞりありで解説してあります。 定規とコンパスを用意してとりくみましょう。 手順は、 ①最初に底辺を同じ長さで書く ②対応する辺と



三角形の相似 合同条件 中学 数学 理科の復習サイト



中学数学 図形の合同 図形の性質
三角形の合同の証明 基本篇(2) このページで、合同の証明を2問解説していきます。 その中で、証明の流れや何故その説明をするのか‥というところも気にしながら読み進めると、さらに力が付きますのでおススメです! 今回紹介するような証明の基本的な問題を何回か解いて、証明問題に 「合同な三角形の書き方」 と同じ内容です もし、忘れていても 大丈夫です 今回でしっかり 覚えましょうね 合同の表し方 ABC≡ DEF 「≡(合同)」と読みます 三角形の合同条件 3組の辺が、それぞれ等しい 2組の辺とその間の角が、それぞれ等しい 1組の辺とその両端の角が、それぞれ等しい 合同な図形の対応する 線分の長さ 角の大きさ はそれぞれ等しくなります 先生、教科書に三角形の合同条件 sss (三辺相等) 3組の辺がそれぞれ等しい。 sas (二辺夾角相等または二辺挟角相等) 2組の辺とその間の角がそれぞれ等しい。 asa (一辺両端角相等/二角夾辺相等) 1組の辺とその両端の角がそれぞれ等しい。




三角形の合同条件 相似条件と合同条件の違いとは アタリマエ



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
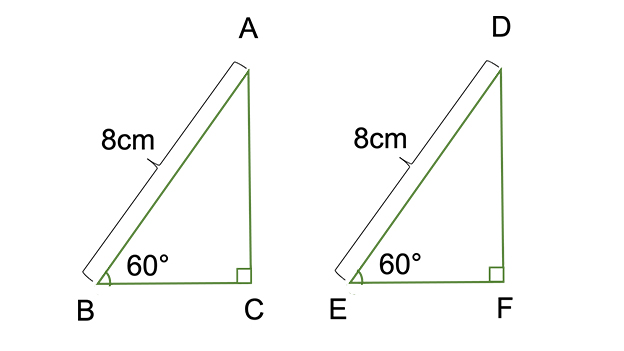
三角形の合同条件より、二辺の長さとその間の角がそれぞれ等しい場合に二つの三角形は合同、と言えます。 したがって、 abc≡ a´b´c´ となります。他の角度に注目した場合についても練習してみて下さい。 角度についても、しっかりと対応させた表現をするようにしてください三角形の合同条件 3組の辺 がそれぞれ等しい 2組の辺 と その間の角 がそれぞれ等しい 1組の辺 とその 両端の角 がそれぞれ等しい 斜辺 と それ以外の辺 がそれぞれ等しい 斜辺 と 1つの鋭角 がそれぞれ等しい ※斜辺: 直角三角形において、直角と向かい合う一番長い辺 ※鋭角: 90°未満の角 合同を証明するには、実際は直角三角形であることも条件に入るため ここには、三角形の合同条件を入れます。ここがしっかり答えられるようにするために、三角形の合同条件を暗記するんですね。 実は、ここに入る合同条件は、ほとんどの場合 ② 2組の辺とその間の角が、それぞれ等しい。 ③ 1組の辺とその両端の角が、それぞれ等しい。 のどちらかなん



3
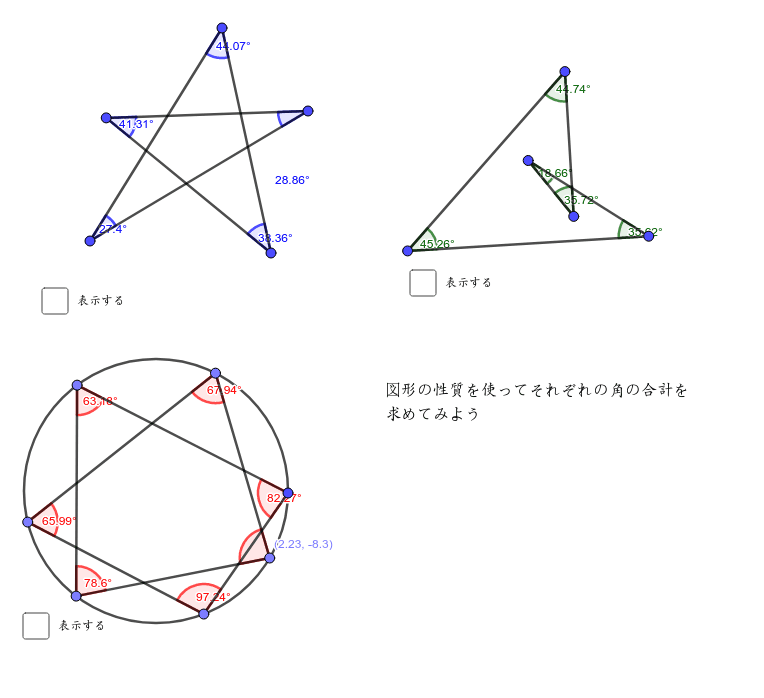



中2 数学 三角形の合同条件 角の和を求めてみよう Geogebra
三角形の合同条件 2つの三角形において、次の3つの条件のうちのどれかが成り立つとき、その三角形は合同であるといえます。 3つの辺がそれぞれ等しい 2辺とその間の角がそれぞれ等しい 1辺とその両端の角がそれぞれ等しい 三角形の合同条件を使った証明問題三角形の合同証明 応用 (直線と内角の和) 図で, ABCは∠BAC=90°,AB=ACの直角二等辺三角形である。 B,Cから頂点Aを通る直線lに垂線をおろし,交点をそれぞれD,Eとする。 ADB≡ CEAを証明せよ。 A B C l D E 仮定を図にかきいれる。 ∠EAC = ∠DBA となる。 ADB≡ CEAとなる。




三角形の相似条件と証明問題の解き方 数学fun




中2数学 三角形の合同を証明する問題 練習編 映像授業のtry It トライイット
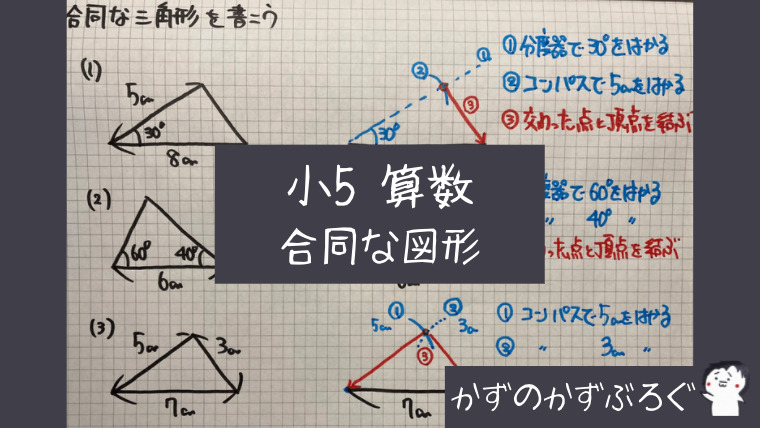



小5算数 合同な図形 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ
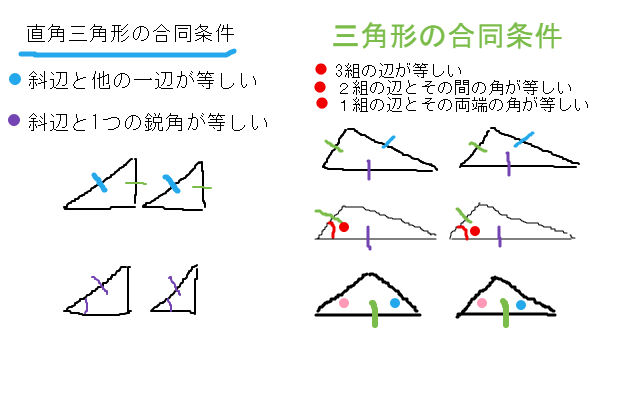



三角形 合同 相似条件 直角三角形の合同条件 中学 数学 理科の復習サイト
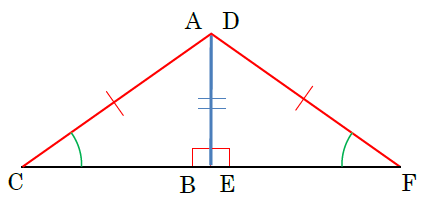



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン By 東京個別指導学院




暗記必須 三角形の合同条件を見やすい図で一発理解しよう 高校生向け受験応援メディア 受験のミカタ




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
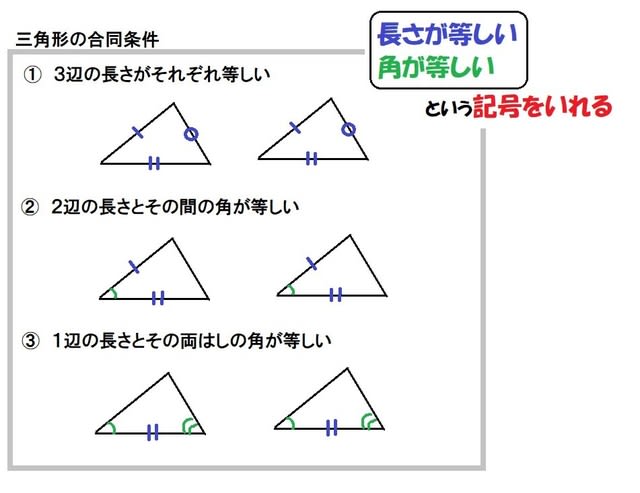



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support




中2 三角形の合同条件 三辺相等 日本語版 Youtube




どの三角形の合同を証明すべきか 17年度北海道 高校入試 数学 良問 難問




三角形の合同条件と証明問題の解き方 数学fun




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン By 東京個別指導学院



File 三角形の合同条件 Png Wikimedia Commons



合同な図形 正三角形の証明問題 苦手な数学を簡単に



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
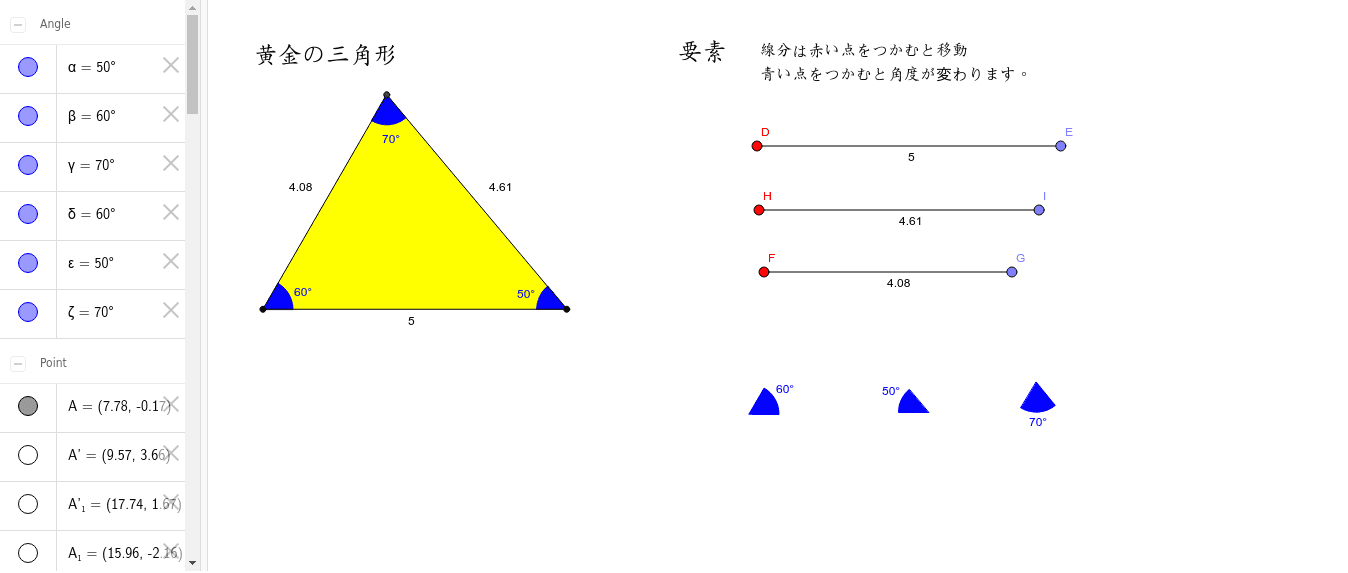



三角形の合同条件を見つける Geogebra




中2 三角形の合同条件の見つけ方 使い方をイチから Youtube



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン By 東京個別指導学院



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン By 東京個別指導学院




中学数学より3 三角形の合同条件 身勝手な主張




図形の合同 Wikipedia




中学数学より3 三角形の合同条件 身勝手な主張
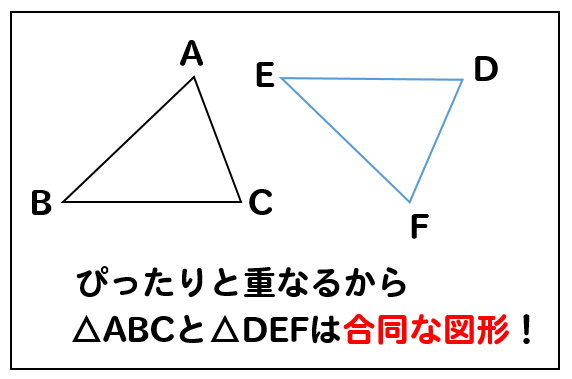



三角形の合同条件 合同な図形の見つけ方 証明問題の基礎を身につけよう 数スタ
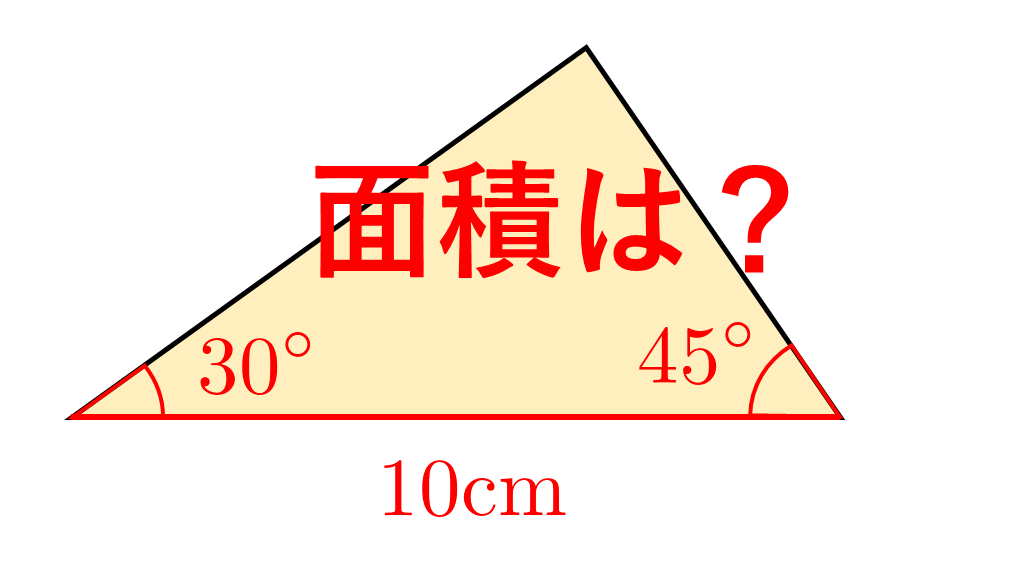



三角形の合同条件と面積 数学 統計教室の和から株式会社



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典
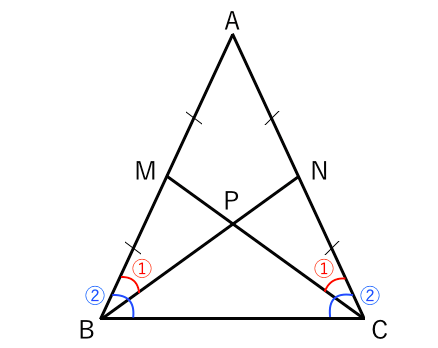



合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典




合同条件について Blogskol
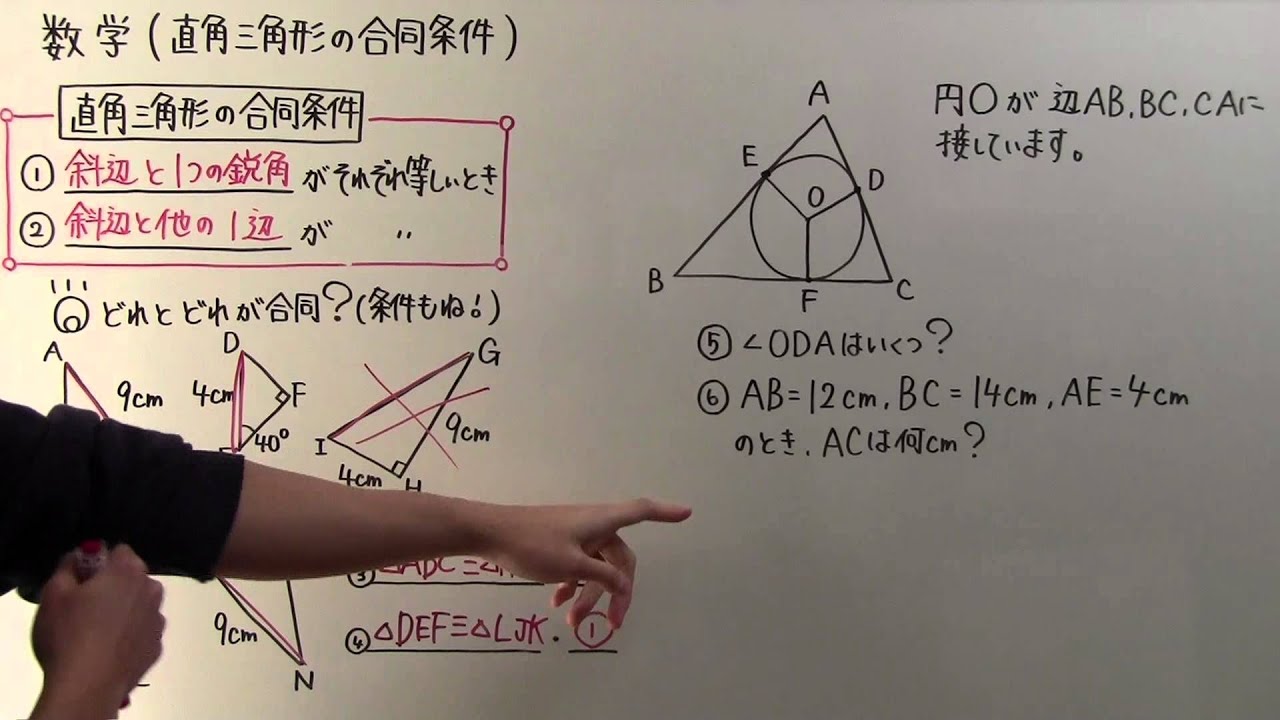



数学 中2 71 直角三角形の合同条件 Youtube



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典




合同な図形の性質 三角形の合同とはどういう意味 Qikeru 学びを楽しくわかりやすく




直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方
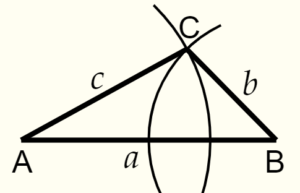



三角形の合同条件を忘れたときは三角形を自分で書いて思い出そう 数学基礎トレーニングルーム



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典
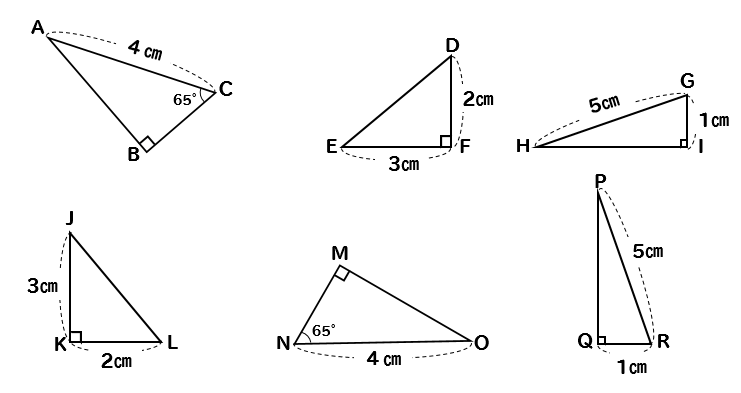



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




夏場だけでもシグマゼミも勉強しに来ませんか そういや 中2の 三角形の合同条件 とかさ 中学でよくある 一字一句この通りに書かないと減点 なものの代表格だと思うんだけど あれ 教科書によってびみょーにちがったりしないの 写真は 学校図書




直角三角形の合同条件とその証明 数学fun
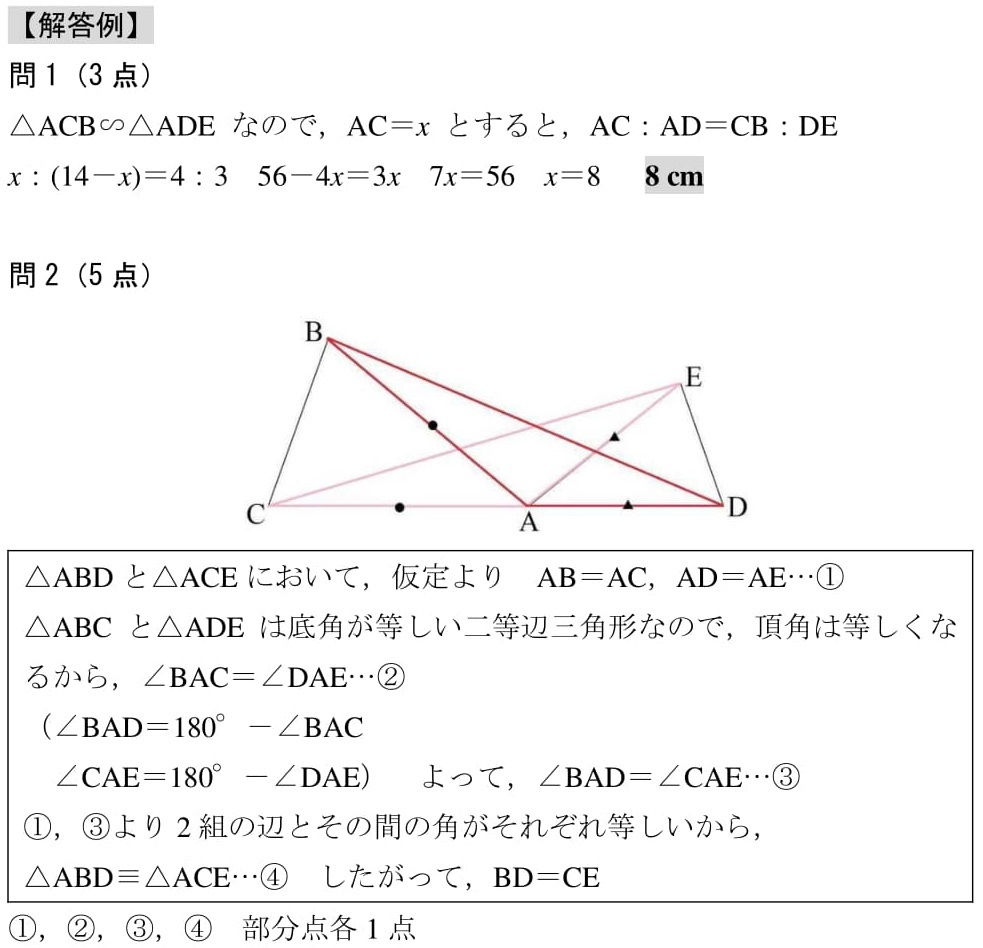



どの三角形の合同を証明すべきか 17年度北海道 高校入試 数学 良問 難問



Studydoctor三角形の合同証明の進め方 中2数学 Studydoctor




直角三角形の合同条件 Youtube
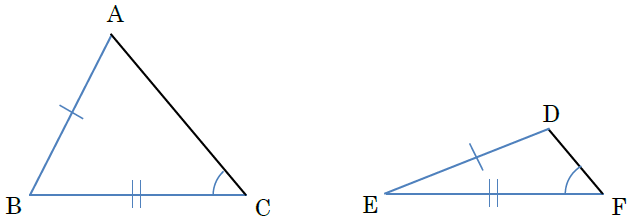



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン By 東京個別指導学院
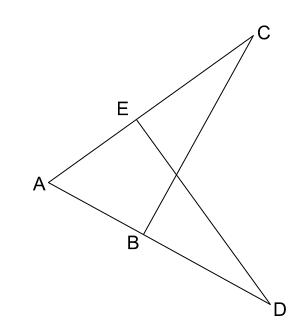



中学数学 三角形の合同の証明 その2 中学数学の無料オンライン学習サイトchu Su



公理から手繰る 三角形の合同条件の証明 二辺挟角 Sas 数学探求 ぱるきちどっとこむ



直角三角形の合同条件とそれを利用した証明 チーム エン



1



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典




三角形の合同の証明はとてもお得なんです セルモ大蔵 世田谷 の塾長ブログ



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン By 東京個別指導学院



直角三角形の合同条件の説明 おかわりドリル



合同な図形とは 三角形の合同条件 教遊者



三角形の合同 理数系学習サイト Kori



中学数学 直角三角形の合同条件 中学数学の無料オンライン学習サイトchu Su



直角三角形の合同条件の説明 おかわりドリル



三角形の合同条件と証明問題の解き方 数学fun




直角三角形の合同条件 証明のときに直角三角形が出てきたらこれ 中学や高校の数学の計算問題




記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス



三角形の合同条件の説明 おかわりドリル
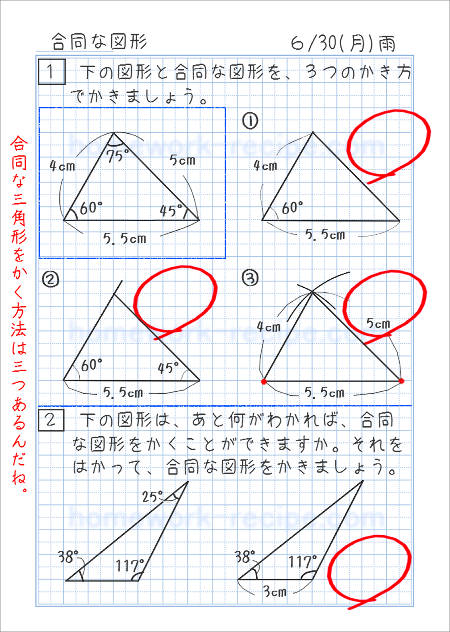



合同な三角形をかこう 家庭学習レシピ




中2 三角形の合同を利用した証明 平戸いの翔塾の塾長ブログ
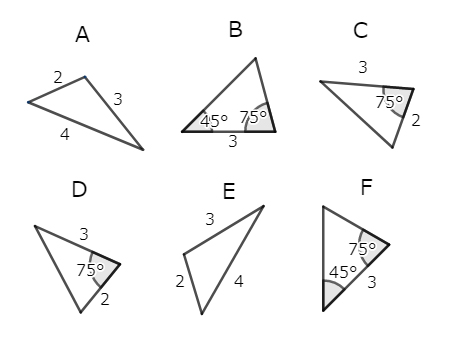



数学のアレ 何に役立つ 三角形の合同条件 同じ形の三角形を見つけて テストで5点くらいもらう 以外の使い方 1 2 ページ ねとらぼ



1



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




数学 中2 56 三角形の合同 基本編 Youtube
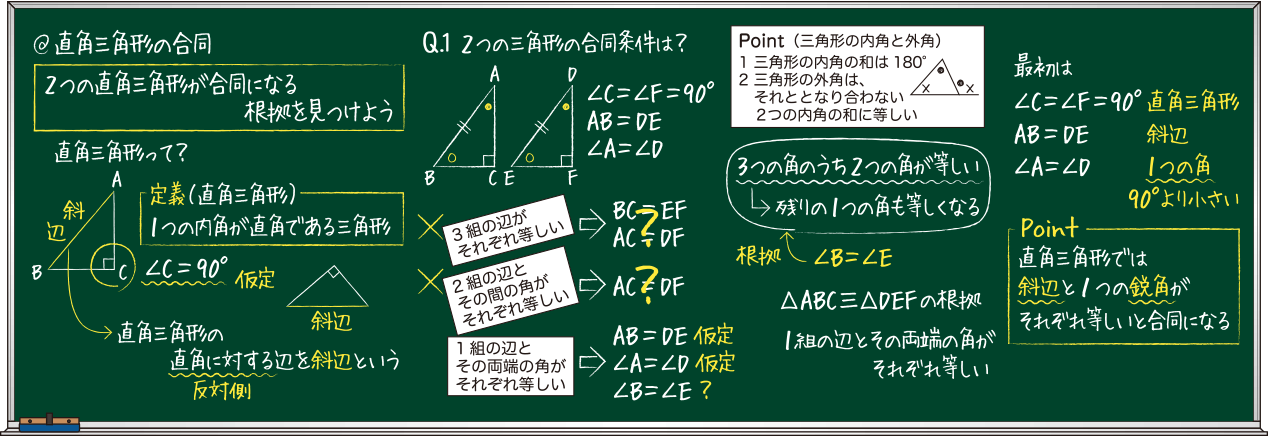



思考を見せる板書例 2年5章 直角三角形になる根拠をみつけよう Math Connect 東京書籍 先生のための算数数学ポータルサイト




中2数学 三角形の合同条件の覚え方と証明問題のポイントを徹底解説 Studysearch



合同な図形とは 三角形の合同条件 教遊者




三角形の合同条件を使った証明問題 中学2年生の問題を解こう 身勝手な主張
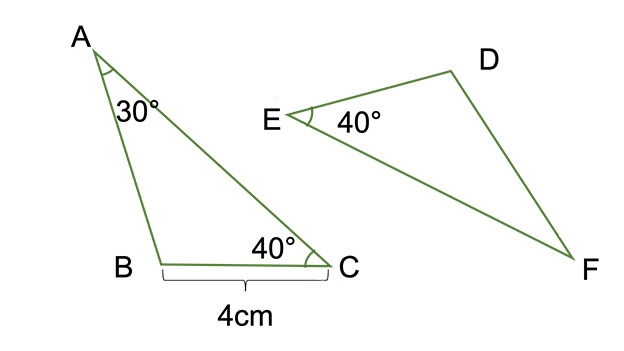



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾
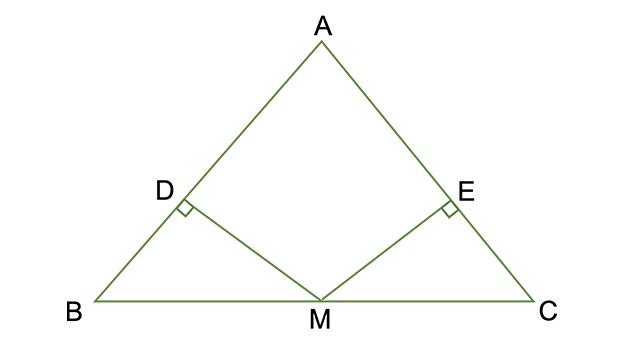



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




三角形の合同条件



1
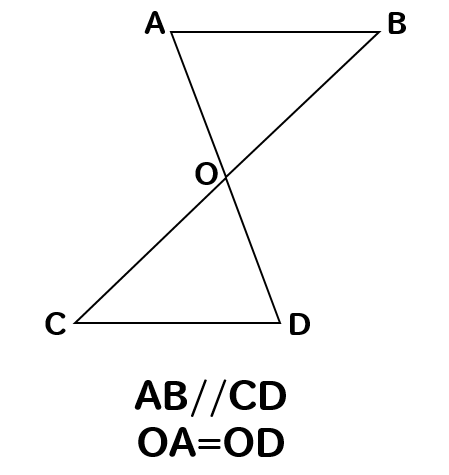



三角形の合同条件 合同な図形の見つけ方 証明問題の基礎を身につけよう 数スタ




直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




直角三角形の合同条件とその証明 数学fun




合同な三角形の書き方 算数 数学が好きになりmath



Studydoctor三角形の合同の証明 応用 中2数学 Studydoctor




暗記必須 三角形の合同条件を見やすい図で一発理解しよう 高校生向け受験応援メディア 受験のミカタ




三角形の合同条件と証明問題の解き方 数学fun




直角三角形の合同 無料で使える中学学習プリント
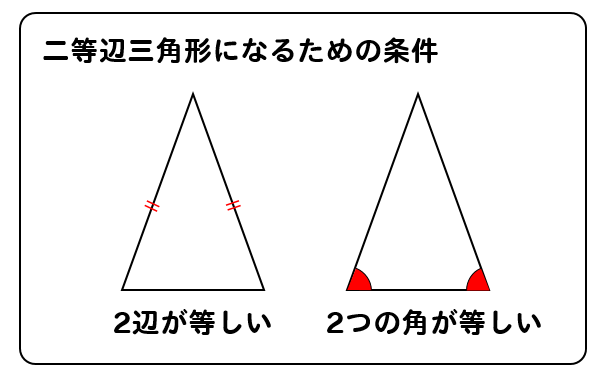



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




三角形の合同と軌跡 Geogebra
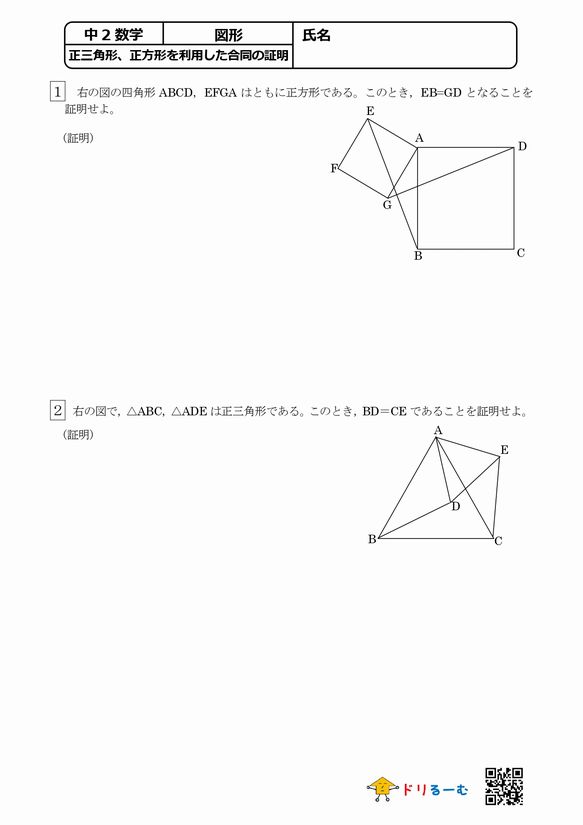



正三角形 正方形を利用した合同の証明 ドリるーむ
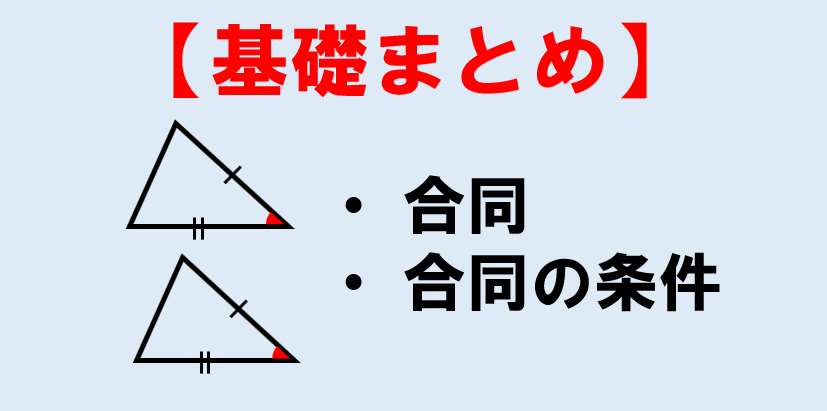



中2数学 合同 三角形の合同条件まとめ 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
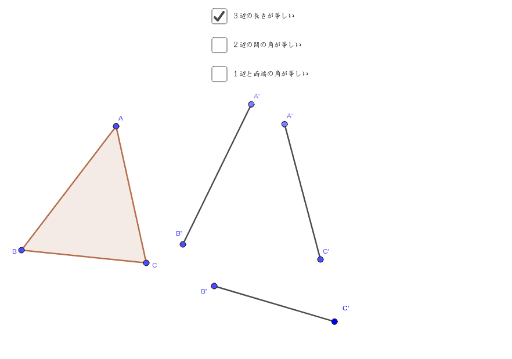



三角形の合同条件 Geogebra




世界一わかりやすい数学問題集中2 4章 平行と合同と証明



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典
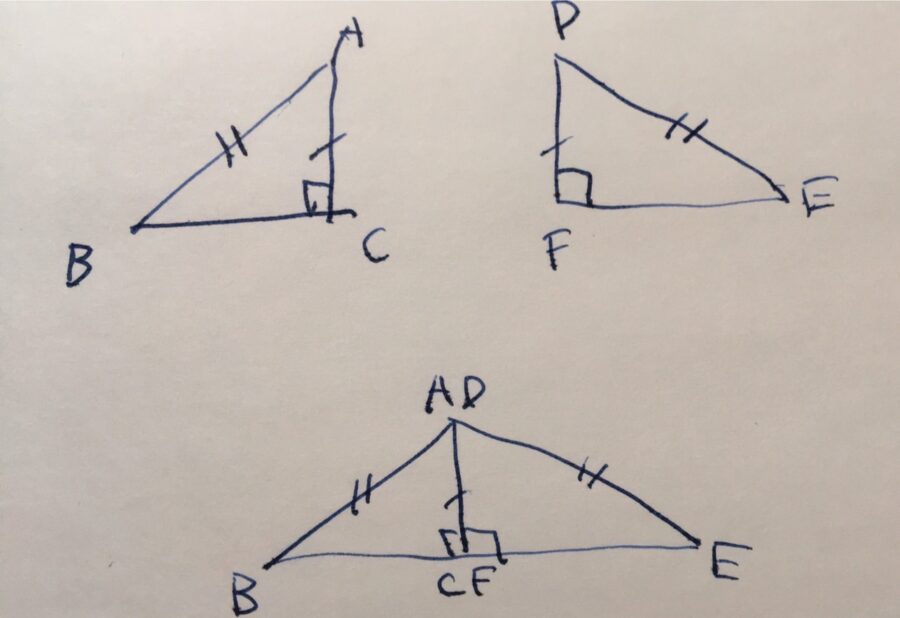



直角三角形の合同条件 斜辺ともう一辺の長さが等しいなら合同 Hl の証明 趣味の大学数学
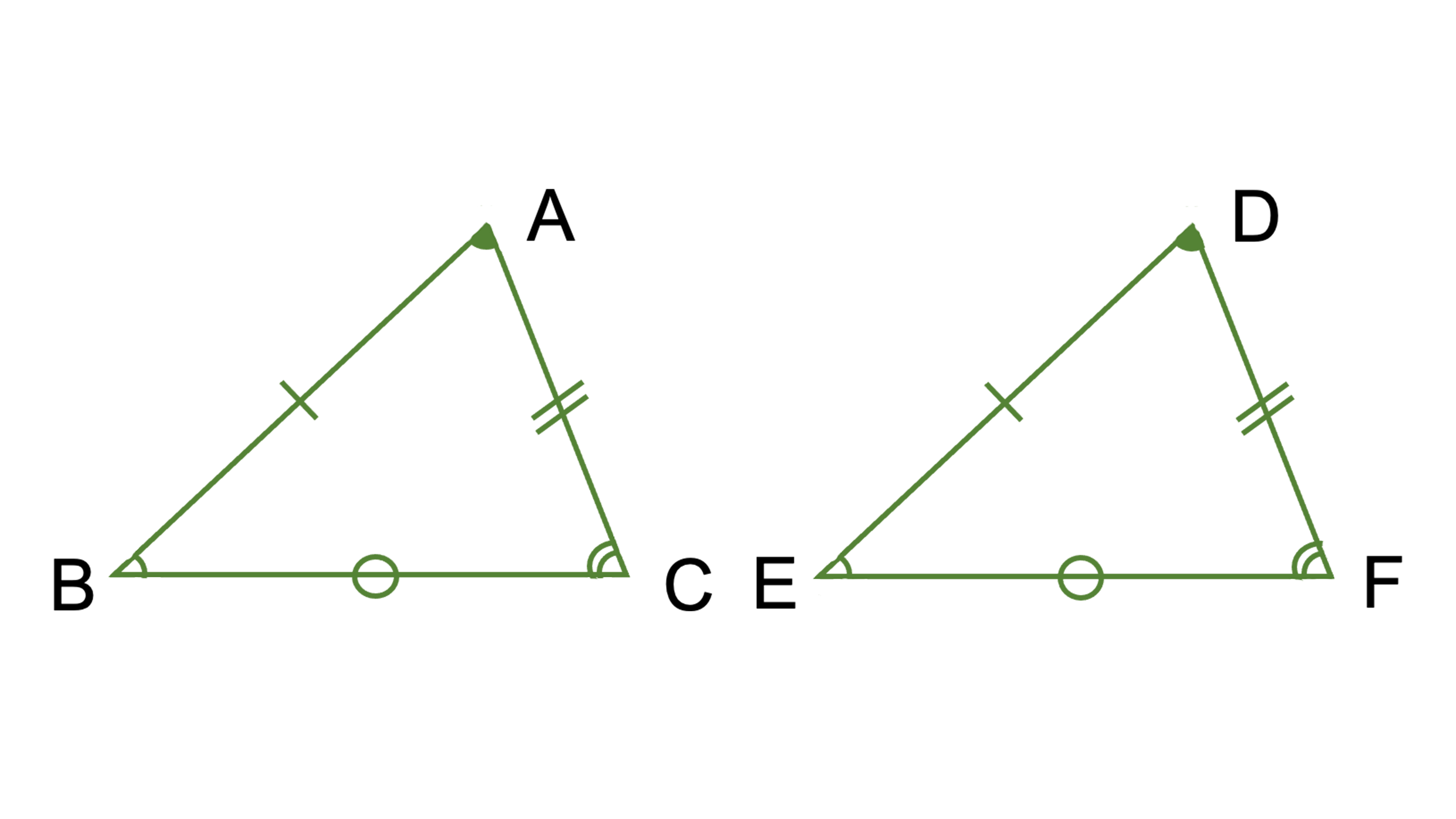



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




直角三角形の合同条件の証明 Youtube




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学



0 件のコメント:
コメントを投稿