
Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集 Waenavi
7章 三平方の定理 25三平方の定理 三平方の定理まとめ、予習&テスト勉強前に中学3年数学 三平方の定理の証明中学3年数学 三平方の定理の計算中学3年数学 三平方の定理の利用中学3年数学 三平方の定理の逆とは中学3年数学 三平方の定理で、残り1辺の計算と、角度の計算をします。・各種条件を入れてください。 (黒色で塗りつぶした場所は、自動計算です)・残り一辺の長さとそれぞれの角度を計算します。 の相場!平米数と購入価格の平均・中央値を確認!
三 平方 の 定理 応用
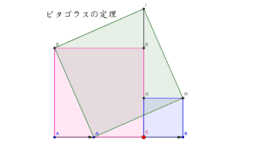
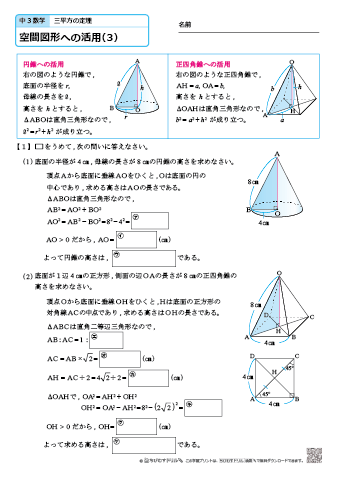
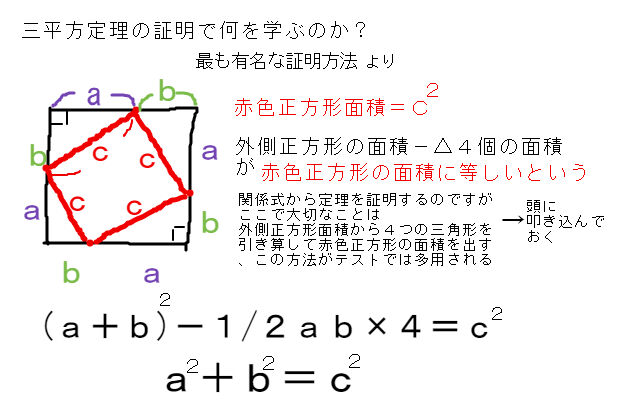
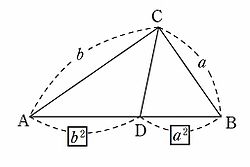
三 平方 の 定理 応用-三平方の定理を直接証明するというものではないので、ややこしく感じるかもしれません。 納得できない人のために、次は図で直感的に理解できるよう解説します。 三平方の定理が直感的にわかる図 三平方の定理は各辺の2乗の等式です。===三平方の定理の応用=== 三平方の定理 次の図のような直角三角形については b2c2=a2 が成り立つ. 三平方の定理を使えば,直角三角形の2辺の長さが分かれば残りの1辺の長さが求められる. たとえば次の図では, b , c が分かっていれば a が求められる. a , c が分かっていれば b が求められる. a , b が分かっていれば c が求められる. 例1 次の図で黄色の三角形について三平方の定理を

Mathematics 三平方の定理 3 いろいろな三角形 働きアリ
三平方の定理の平面図形への利用ですが、小学生や中学1年生、2年生で習った内容も含みますので、図形の基本的な性質を思い出しましょう。 また、暗記をしてしまった方がラクに解けるような問題もありますので、下の説明で 要暗記 の部分は暗記し 受験勉強のコツです。 受験の数学で必須項目の一つに「三平方の定理」があります。 a 2 b 2 = c 2 です。 (ここで、直角に対する辺cが斜辺です。 ) 図1:直角三角形。 90゜に対する辺cが、斜辺。 さらに、応用問題でよく利用される辺の比があります。おさらいとして三平方の定理は以下の通り。 これに対して、逆も成り立ちます。 三角形の各辺に関して、 c2 = a2 b2 c 2 = a 2 b 2 という関係にあるなら、その三角形は直角三角形であるといえます。 そして、以下の2種類の直角三角形を覚える必要があります。 これらの角の大きさと辺の比をしっかり対応させましょう。 それぞれの辺の比は二等辺三角形・正三角形の性質から導けますが、
・直角三角形 ⇒ ならば(斜辺c)2 = (隣辺a)2 (対辺b)2 ・ (最大の辺) 2 = (他の辺) 2 (他の辺)2 ⇒ ならば直角三角形 cf 直角三角形の辺の名前 ∠θを基準に、 隣にあるのが 隣辺 対面にあるのが 対辺 ですが中学では、「斜辺」と「それ以外」で十分ですね これだけです! 直角三角形 の3辺のうち、 2辺が判れば残りの1辺がわか三平方の定理に当てはめて求める問題です。平方根が出てくる場合が多いので、平方根の計算も同時に覚えましょう。 斜辺以外の一辺の長さを求める場合は、三平方の定理を式変形して a² = c² – b² = (cb)(cb) を用いると簡単に解けます。三平方の定理応用(面積) 三平方の定理の平面図形の応用問題です。 入試にもよく出題される問題をアップしていきます。 定期テスト対策、高校入試対策の問題として利用してください。
三 平方 の 定理 応用のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
私の彼はエプロン男子 キャスト相関図。登場人物と出演者一覧。 Catch! 日常生活とすれば,三平方の定理は確かに我々の身の回り日常生活の中で使われています. 数学はいわゆる「役立つ」ものとは限らないとも思いますが, 余り気付かないものですが,ふと見渡せばこういう面で日常に多々役立てられているものです. 4





0 件のコメント:
コメントを投稿